Multimediaexpo.cz je již 18 let na českém internetu !!
V tiskové zprávě k 18. narozeninám brzy najdete nové a zásadní informace.
Nezávislá množina
Z Multimediaexpo.cz
(+ Masivní vylepšení) |
m (Nahrazení textu „<math>“ textem „<big>\(“) |
||
| Řádka 5: | Řádka 5: | ||
== Definice == | == Definice == | ||
| - | Nechť ''G = (V, E)'' je graf, pak < | + | Nechť ''G = (V, E)'' je graf, pak <big>\(S \subseteq V</math> je ''nezávislá množina'', pokud platí <big>\(\forall x, y \; \in S: (x, y) \notin E</math>. |
=== Nezávislost grafu === | === Nezávislost grafu === | ||
| - | Nezávislost grafu G (značíme < | + | Nezávislost grafu G (značíme <big>\(\alpha(G)</math> )je největší počet prvků nezávislé množiny grafu G. |
== Maximální nezávislá množina == | == Maximální nezávislá množina == | ||
Verze z 14. 8. 2022, 14:48
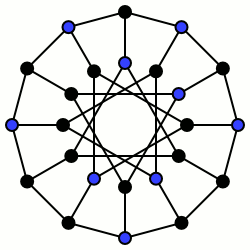
Nezávislá množina (NM) je pojem z teorie grafů. Nezávislá množina v grafu je taková množina jeho vrcholů, že žádné dva z nich nejsou spojeny hranou.
Definice
Nechť G = (V, E) je graf, pak \(S \subseteq V</math> je nezávislá množina, pokud platí \(\forall x, y \; \in S: (x, y) \notin E</math>.
Nezávislost grafu
Nezávislost grafu G (značíme \(\alpha(G)</math> )je největší počet prvků nezávislé množiny grafu G.
Maximální nezávislá množina
Častou úlohou v teorii grafů je hledání maximální nezávislé množiny daného grafu. Ukazuje se ovšem, že je to NP-úplný problém. Důkaz se provádí polynomiálním převodem instance problému maximální kliky v grafu na instanci problému NM (hledání nezávislé množiny velikosti k odpovídá hledání kliky velikosti k v doplňkovém grafu). Pokud by bylo možné řešit tento problém deterministicky v polynomiálním čase, bylo by tak možné řešit i problém kliky, o kterém je dokázáno, že je NP-úplný.
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |