Motorem našeho webového serveru bude pekelně rychlý
procesor AMD Ryzen Threadripper 7960X (ZEN 4).
Komplexní rovina
Z Multimediaexpo.cz
(+ Nový článek...) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| (Nejsou zobrazeny 3 mezilehlé verze.) | |||
| Řádka 1: | Řádka 1: | ||
| - | + | '''Komplexní rovina''' (často též '''Gaussova rovina''') je v [[matematika|matematice]] způsob zobrazení [[komplexní číslo|komplexních čísel]]. Ve frankofonní literatuře bývá někdy označována jako '''Argandova rovina''', Cauchyho rovina nebo '''Argandův diagram'''. | |
| + | Na [[osa|osu]] ''x'' se vynáší reálná část komplexního čísla ''z'', tzn. <big>\(x = \mathrm{Re}(z)\)</big>, a proto je tato osa označována jako '''reálná'''. | ||
| + | |||
| + | Na osu ''y'' se vynáší imaginární část komplexního čísla ''z'', tzn. <big>\(y = \mathrm{Im}(z)\)</big>, a proto je tato osa označována jako '''imaginární'''. | ||
| + | |||
| + | Komplexní rovinu, do níž zahrnujeme i nevlastní bod <big>\(z = \infty\)</big>, označujeme jako ''rozšířenou rovinu (komplexních čísel)''. Tato zúplněná komplexní čísla však názorněji zobrazuje [[Riemannova koule]]. | ||
| + | |||
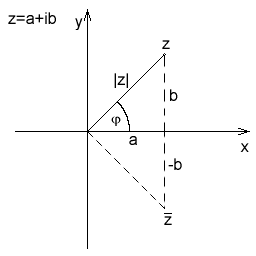
| + | Na obrázku je zobrazen vztah mezi komplexním číslem a [[komplexně sdružené číslo|číslem sdruženým]] v komplexní rovině. | ||
| + | |||
| + | [[Soubor:komplexni_rovina.png|Zobrazení komplexního čísla v komplexní rovině.]] | ||
| + | |||
| + | Znázorňujeme-li čísla tímto způsobem, pak součet dvou čísel odpovídá [[vektorový součet|vektorovému součtu]] jejich průvodičů (tzv. rovnoběžníkové pravidlo). | ||
| + | |||
| + | Při násobení je argument součinu roven součtu argumentů jednotlivých činitelů a [[absolutní hodnota]] výsledku je rovna součinu absolutních hodnot násobených čísel. To geometricky odpovídá přímé podobnosti - otočení okolo počátku složenému se stejnolehlostí se středem v počátku. | ||
| + | |||
| + | == Související články == | ||
| + | * [[Komplexní číslo]] | ||
| + | * [[Riemannova koule]] | ||
| + | |||
| + | |||
| + | {{Článek z Wikipedie}} | ||
[[Kategorie:Komplexní čísla]] | [[Kategorie:Komplexní čísla]] | ||
[[Kategorie:Komplexní analýza]] | [[Kategorie:Komplexní analýza]] | ||
| + | [[Kategorie:Diagramy]] | ||
Aktuální verze z 14. 8. 2022, 14:52
Komplexní rovina (často též Gaussova rovina) je v matematice způsob zobrazení komplexních čísel. Ve frankofonní literatuře bývá někdy označována jako Argandova rovina, Cauchyho rovina nebo Argandův diagram.
Na osu x se vynáší reálná část komplexního čísla z, tzn. \(x = \mathrm{Re}(z)\), a proto je tato osa označována jako reálná.
Na osu y se vynáší imaginární část komplexního čísla z, tzn. \(y = \mathrm{Im}(z)\), a proto je tato osa označována jako imaginární.
Komplexní rovinu, do níž zahrnujeme i nevlastní bod \(z = \infty\), označujeme jako rozšířenou rovinu (komplexních čísel). Tato zúplněná komplexní čísla však názorněji zobrazuje Riemannova koule.
Na obrázku je zobrazen vztah mezi komplexním číslem a číslem sdruženým v komplexní rovině.
Znázorňujeme-li čísla tímto způsobem, pak součet dvou čísel odpovídá vektorovému součtu jejich průvodičů (tzv. rovnoběžníkové pravidlo).
Při násobení je argument součinu roven součtu argumentů jednotlivých činitelů a absolutní hodnota výsledku je rovna součinu absolutních hodnot násobených čísel. To geometricky odpovídá přímé podobnosti - otočení okolo počátku složenému se stejnolehlostí se středem v počátku.
Související články
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |