Kruh

Z Multimediaexpo.cz

(Rozdíly mezi verzemi)
(šablony)
m (Nahrazení textu „</math>“ textem „\)</big>“)
 
(Nejsou zobrazeny 2 mezilehlé verze.)
Řádka 4: Řádka 4:
== Základní vzorce ==
== Základní vzorce ==
Obvod '''o''' kruhu je určen vzorcem
Obvod '''o''' kruhu je určen vzorcem
-
:<math>o = 2 \pi r\,</math>
+
:<big>\(o = 2 \pi r\,\)</big>
jeho plocha '''S''' vzorcem
jeho plocha '''S''' vzorcem
-
:<math>S = \pi r^2.\ </math>
+
:<big>\(S = \pi r^2.\ \)</big>
== Další pojmy ==
== Další pojmy ==
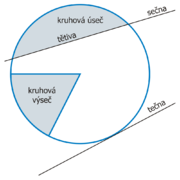
Část kruhu, vymezená dvěma průvodiči, je '''[[kruhová výseč]]''', část kruhu, omezená sečnou, je '''[[kruhová úseč]]'''. Plocha vymezená dvěma soustřednými kružnicemi o nestejném poloměru je '''[[mezikruží]]'''.
Část kruhu, vymezená dvěma průvodiči, je '''[[kruhová výseč]]''', část kruhu, omezená sečnou, je '''[[kruhová úseč]]'''. Plocha vymezená dvěma soustřednými kružnicemi o nestejném poloměru je '''[[mezikruží]]'''.

Aktuální verze z 14. 8. 2022, 14:52

Kruh


Kruh je rovinný geometrický útvar, omezený kružnicí. Kruh je určen svým středem S a poloměrem r: je to množina všech bodů roviny, které mají od středu vzdálenost menší nebo rovnou poloměru.

Obsah

Základní vzorce

Obvod o kruhu je určen vzorcem

\(o = 2 \pi r\,\)

jeho plocha S vzorcem

\(S = \pi r^2.\ \)

Další pojmy

Část kruhu, vymezená dvěma průvodiči, je kruhová výseč, část kruhu, omezená sečnou, je kruhová úseč. Plocha vymezená dvěma soustřednými kružnicemi o nestejném poloměru je mezikruží.

Kvadratura kruhu

Kvadratura kruhu - úloha najít čtverec, jehož plocha se rovná ploše daného kruhu - není prostředky elementární geometrie řešitelná. Přibližná řešení byla ovšem známa už ve starověku.

Odkazy

Související články

Externí odkazy


Flickr.com nabízí fotografie, obrázky a videa k tématu
Kruh
Commons nabízí fotografie, obrázky a videa k tématu
Kruh
Citováno z „http://ww.multimediaexpo.cz/mmecz/index.php/Kruh“