V sobotu 2. listopadu proběhla mohutná oslava naší plnoletosti !!
Multimediaexpo.cz je již 18 let na českém internetu !!

Simplex

Z Multimediaexpo.cz

(Rozdíly mezi verzemi)
(+ Aktualizace)
m (Nahrazení textu „</math>“ textem „\)</big>“)
 
(Není zobrazena jedna mezilehlá verze.)
Řádka 1: Řádka 1:
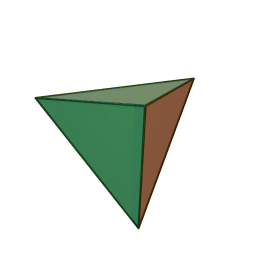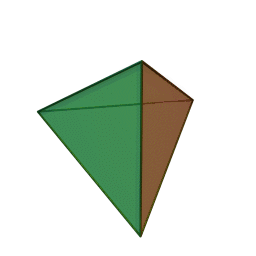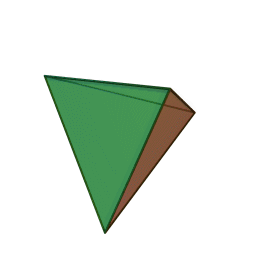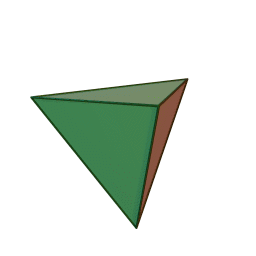
[[Soubor:Tetrahedron.gif|thumb|256px|Čtyřstěn – 3simplex]]
[[Soubor:Tetrahedron.gif|thumb|256px|Čtyřstěn – 3simplex]]
-
'''Simplex''' (či '''''n''-simplex''') je ''n''-[[Dimenze vektorového prostoru|rozměrným]] zobecněním [[trojúhelník]]u. Jedná se o [[konvexní obal]] [[množina|množiny]] <math>{n+1}</math> [[afinní transformace souřadnic|afinně nezávislých]] [[bod]]ů umístěný v [[Eukleidovský prostor|euklidovském prostoru]] [[Dimenze vektorového prostoru|dimenze]] <math>n</math> či vyšší.
+
'''Simplex''' (či '''''n''-simplex''') je ''n''-[[Dimenze vektorového prostoru|rozměrným]] zobecněním [[trojúhelník]]u. Jedná se o [[konvexní obal]] [[množina|množiny]] <big>\({n+1}\)</big> [[afinní transformace souřadnic|afinně nezávislých]] [[bod]]ů umístěný v [[Eukleidovský prostor|euklidovském prostoru]] [[Dimenze vektorového prostoru|dimenze]] <big>\(n\)</big> či vyšší.
Například 0simplex je [[bod]], 1simplex je [[úsečka]], 2simplex je [[trojúhelník]], 3simplex je [[čtyřstěn]] (tetraedr), 4simplex je [[pentachoron]] (vždy včetně vnitřku).
Například 0simplex je [[bod]], 1simplex je [[úsečka]], 2simplex je [[trojúhelník]], 3simplex je [[čtyřstěn]] (tetraedr), 4simplex je [[pentachoron]] (vždy včetně vnitřku).
Řádka 7: Řádka 7:
Následující vzorce udávají geometrické vlastnosti ''n''-simplexu s délkou hrany ''a''.
Následující vzorce udávají geometrické vlastnosti ''n''-simplexu s délkou hrany ''a''.
-
* Výška: <math> \sqrt{n+1 \over 2 n} a </math>
+
* Výška: <big>\( \sqrt{n+1 \over 2 n} a \)</big>
-
* Objem: <math> {\sqrt{n+1} \over n! \sqrt{2^n}} a^n </math>
+
* Objem: <big>\( {\sqrt{n+1} \over n! \sqrt{2^n}} a^n \)</big>
{{Článek z Wikipedie}}
{{Článek z Wikipedie}}
[[Kategorie:Geometrie]]
[[Kategorie:Geometrie]]

Aktuální verze z 14. 8. 2022, 14:53

Čtyřstěn – 3simplex

Simplex (či n-simplex) je n-rozměrným zobecněním trojúhelníku. Jedná se o konvexní obal množiny \({n+1}\) afinně nezávislých bodů umístěný v euklidovském prostoru dimenze \(n\) či vyšší.

Například 0simplex je bod, 1simplex je úsečka, 2simplex je trojúhelník, 3simplex je čtyřstěn (tetraedr), 4simplex je pentachoron (vždy včetně vnitřku).

Geometrie

Následující vzorce udávají geometrické vlastnosti n-simplexu s délkou hrany a.

  • Výška: \( \sqrt{n+1 \over 2 n} a \)
  • Objem: \( {\sqrt{n+1} \over n! \sqrt{2^n}} a^n \)


Citováno z „http://ww.multimediaexpo.cz/mmecz/index.php/Simplex“