Multimediaexpo.cz je již 18 let na českém internetu !!
Hrana (geometrie)
Z Multimediaexpo.cz
m (1 revizi) |
(+ Masivní vylepšení) |
||
| (Není zobrazena jedna mezilehlá verze.) | |||
| Řádka 1: | Řádka 1: | ||
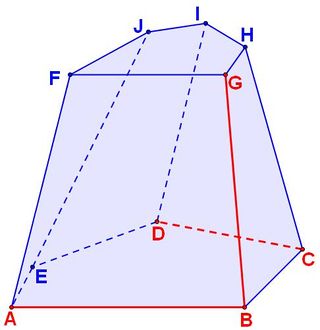
| - | + | [[File:Polyhedron edges.JPG|thumb|320px|Mnohostěn ABCDEFGHIJ s vyznačenými hranami AB, CD, BG]] | |
| + | '''Hrana''' je v [[geometrie|geometrii]] [[úsečka]], tvořená [[průnik]]em dvou sousedních [[stěna (geometrie)|stěn]] [[mnohostěn]]u. [[Bod]]y, ve kterých se setkávají (nejméně 3) hrany, se nazývají [[vrchol (geometrie)|vrcholy]]. | ||
| + | == Popis hran == | ||
| + | Hrany se označují malými písmeny. Délka hrany se označuje stejně jako velikost úsečky: ''|AB|'' tedy značí velikost strany ''AB''. Označení souvisejících útvarů je obdobné jako u úsečky – střed hrany je bod, který má od obou vrcholů stejnou vzdálenost, osa hrany je kolmice, procházející jejím středem. Každá hrana má nekonečně mnoho os. | ||
| + | |||
| + | == Vlastnosti hran == | ||
| + | Počet hran (''h'') konvexního mnohostěnu určíme, pokud známe počet jeho vrcholů (''V'') a stěn (''s'') pomocí tzv. ''Eulerovy věty'': | ||
| + | |||
| + | <big>V - h + s = 2</big> | ||
| + | |||
| + | Nejméně hran ze všech mnohostěnů má [[čtyřstěn]] – 6. | ||
| + | |||
| + | Hrana může být také [[přímka]] nebo [[polopřímka]] – např. pokud mají dvě různoběžné poloroviny společnou hraniční přímku (vytvářejí [[poloprostor|prostorový klín]]), označujeme ji jako '''hranu klínového prostoru'''. | ||
| + | |||
| + | == Souvisejí články == | ||
| + | *[[Těleso]] | ||
| + | *[[Mnohostěn]] | ||
| + | *[[Vrchol (geometrie)]] | ||
| + | *[[Strana (geometrie)]] | ||
| + | *[[Stěna (geometrie)]] | ||
| + | |||
| + | == Externí odkazy == | ||
| + | |||
| + | {{Článek z Wikipedie}} | ||
[[Kategorie:Geometrie]] | [[Kategorie:Geometrie]] | ||
Aktuální verze z 23. 9. 2014, 19:34
Hrana je v geometrii úsečka, tvořená průnikem dvou sousedních stěn mnohostěnu. Body, ve kterých se setkávají (nejméně 3) hrany, se nazývají vrcholy.
Obsah |
Popis hran
Hrany se označují malými písmeny. Délka hrany se označuje stejně jako velikost úsečky: |AB| tedy značí velikost strany AB. Označení souvisejících útvarů je obdobné jako u úsečky – střed hrany je bod, který má od obou vrcholů stejnou vzdálenost, osa hrany je kolmice, procházející jejím středem. Každá hrana má nekonečně mnoho os.
Vlastnosti hran
Počet hran (h) konvexního mnohostěnu určíme, pokud známe počet jeho vrcholů (V) a stěn (s) pomocí tzv. Eulerovy věty:
V - h + s = 2
Nejméně hran ze všech mnohostěnů má čtyřstěn – 6.
Hrana může být také přímka nebo polopřímka – např. pokud mají dvě různoběžné poloroviny společnou hraniční přímku (vytvářejí prostorový klín), označujeme ji jako hranu klínového prostoru.
Souvisejí články
Externí odkazy
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |