C2 kubická interpolace
Z Multimediaexpo.cz
m (1 revizi) |
(+ Masivní vylepšení) |
||
| (Není zobrazena jedna mezilehlá verze.) | |||
| Řádka 1: | Řádka 1: | ||
| - | {{ | + | {{Upravit}} |
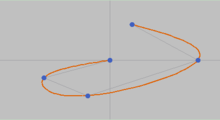
| + | [[Soubor:C2spline.png|thumb|220px|Příklad C2 kubické spline křivky]] | ||
| + | [[Soubor:Interpolacni_kub_spline_krivka.jpg|thumb|220px|Interpolační kubická spline křivka]] | ||
| + | Splajny byly studovány už začátkem [[20. století]]. Označení „spline“ použil poprvé v roce 1946 Shoenberg. Původně byla tímto názvem označována speciální pružná dřevěná nebo kovová pravítka, kterých používali konstruktéři, když při vytváření návrhů trupů lodí potřebovali zadanými body proložit hladkou křivku. | ||
| + | C2 kubická [[interpolace]] patří do skupiny interpolací křivek po obloucích, tj. každý úsek mezi dvěma opěrnými body se interpoluje zvlášť. Pro C2 interpolační křivku musí být zabezpečena C2 [[spojitost]], tj. až do řádu 2. | ||
| + | |||
| + | (U [[C1 kubická interpolace|C1 kubické interpolace]] postačuje spojitost pouze do první derivace křivky.) | ||
| + | |||
| + | == Související == | ||
| + | * [[Geometrie]] | ||
| + | |||
| + | == Externí odkazy == | ||
| + | |||
| + | {{Článek z Wikipedie}} | ||
[[Kategorie:Geometrie]] | [[Kategorie:Geometrie]] | ||
Aktuální verze z 16. 10. 2014, 07:51
Splajny byly studovány už začátkem 20. století. Označení „spline“ použil poprvé v roce 1946 Shoenberg. Původně byla tímto názvem označována speciální pružná dřevěná nebo kovová pravítka, kterých používali konstruktéři, když při vytváření návrhů trupů lodí potřebovali zadanými body proložit hladkou křivku.
C2 kubická interpolace patří do skupiny interpolací křivek po obloucích, tj. každý úsek mezi dvěma opěrnými body se interpoluje zvlášť. Pro C2 interpolační křivku musí být zabezpečena C2 spojitost, tj. až do řádu 2.
(U C1 kubické interpolace postačuje spojitost pouze do první derivace křivky.)
Související
Externí odkazy
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |