Úhlopříčka
Z Multimediaexpo.cz
(Rozdíly mezi verzemi)
(++) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| (Není zobrazena jedna mezilehlá verze.) | |||
| Řádka 6: | Řádka 6: | ||
* úhlopříčka stěnová - leží v některé stěně mnohoúhelníku: '''''B' - D'''''' | * úhlopříčka stěnová - leží v některé stěně mnohoúhelníku: '''''B' - D'''''' | ||
Počet úhlopříček v mnohoúhelníku je možno vypočítat podle vzorce: | Počet úhlopříček v mnohoúhelníku je možno vypočítat podle vzorce: | ||
| - | < | + | <big>\(\frac{n\cdot(n-3)}{2}\)</big>, |
kde n je počet vrcholů mnohoúhelníku | kde n je počet vrcholů mnohoúhelníku | ||
Délka úhlopříčky se často dá spočítat pomocí [[Pythagorova věta|Pythagorovy věty]]. | Délka úhlopříčky se často dá spočítat pomocí [[Pythagorova věta|Pythagorovy věty]]. | ||
Aktuální verze z 14. 8. 2022, 14:54
| Tento článek potřebuje úpravy. Můžete Multimediaexpo.cz pomoci tím, že ho vylepšíte. Jak by měly články vypadat, popisují stránky Vzhled a styl a Encyklopedický styl. |
|
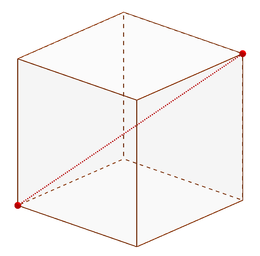
Úhlopříčka (též diagonála) je úsečka, která spojuje dva různé nesousední vrcholy mnohoúhelníka nebo mnohostěnu.
- úhlopříčka tělesová - prochází vnitřkem tělesa: A' - C
- úhlopříčka stěnová - leží v některé stěně mnohoúhelníku: B' - D'
Počet úhlopříček v mnohoúhelníku je možno vypočítat podle vzorce: \(\frac{n\cdot(n-3)}{2}\), kde n je počet vrcholů mnohoúhelníku Délka úhlopříčky se často dá spočítat pomocí Pythagorovy věty. Pomocí úhlopříček lze určit, zda je mnohoúhelník konvexní či nekonvexní. Pokud všechny body úhlopříček náleží mnohoúhelníku, je mnohoúhelník konvexní, pokud ne, je nekonvexní.
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |