Eulerovský graf
Z Multimediaexpo.cz
(Rozdíly mezi verzemi)
(+ Nový článek) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| (Není zobrazena jedna mezilehlá verze.) | |||
| Řádka 6: | Řádka 6: | ||
== Nakreslení Eulerovského grafu == | == Nakreslení Eulerovského grafu == | ||
Libovolný Eulerovský graf lze nakreslit pomocí '''Flueryho algoritmu''', (volně řečeno "jedním tahem"): | Libovolný Eulerovský graf lze nakreslit pomocí '''Flueryho algoritmu''', (volně řečeno "jedním tahem"): | ||
| - | * Vstupem tohoto algoritmu je graf < | + | * Vstupem tohoto algoritmu je graf <big>\(G = (V, H)\)</big> |
| - | * < | + | * <big>\(u\)</big>, <big>\(v\)</big> jsou počáteční a koncový uzel tahu |
* Všechny uzly tohoto grafu jsou: | * Všechny uzly tohoto grafu jsou: | ||
| - | ** Sudého stupně, pak (< | + | ** Sudého stupně, pak (<big>\(u = v\)</big>, tj. tah končí ve stejném místě jako začal) |
| - | ** Právě dva uzly jsou lichého stupně. (< | + | ** Právě dva uzly jsou lichého stupně. (<big>\(u <> v\)</big>). Tah poté vede z uzlu <big>\(u\)</big> ([[Stupeň vrcholu|deg]](u) = lichý) do uzlu <big>\(v\)</big> (deg(v) = lichý) |
| - | * Začínáme v uzlu < | + | * Začínáme v uzlu <big>\(u\)</big> |
| - | * Odebereme(tj. nakreslíme) vždy hranu < | + | * Odebereme(tj. nakreslíme) vždy hranu <big>\(e = (u, w)\)</big> tak, aby po jejím odebrání nebyl zbývající graf rozdělen na několik komponent. Tj. aby zůstal souvislý a přesuneme se na druhou stranu této hrany <big>\(w\)</big>. Opakujeme tento krok dokud je co odebírat. |
== Související články == | == Související články == | ||
Aktuální verze z 14. 8. 2022, 14:51
Eulerovský graf (zkráceně E-graf) je takový souvislý neorientovaný graf, který má všechny uzly sudého stupně. Proto existuje uzavřený tah obsahující všechny jeho hrany.[1]
Orientovaný graf je Eulerovský, existuje-li uzavřený tah obsahující všechny jeho hrany.
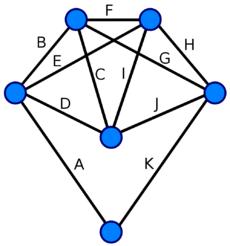
Nakreslení Eulerovského grafu
Libovolný Eulerovský graf lze nakreslit pomocí Flueryho algoritmu, (volně řečeno "jedním tahem"):
- Vstupem tohoto algoritmu je graf \(G = (V, H)\)
- \(u\), \(v\) jsou počáteční a koncový uzel tahu
- Všechny uzly tohoto grafu jsou:
- Sudého stupně, pak (\(u = v\), tj. tah končí ve stejném místě jako začal)
- Právě dva uzly jsou lichého stupně. (\(u <> v\)). Tah poté vede z uzlu \(u\) (deg(u) = lichý) do uzlu \(v\) (deg(v) = lichý)
- Začínáme v uzlu \(u\)
- Odebereme(tj. nakreslíme) vždy hranu \(e = (u, w)\) tak, aby po jejím odebrání nebyl zbývající graf rozdělen na několik komponent. Tj. aby zůstal souvislý a přesuneme se na druhou stranu této hrany \(w\). Opakujeme tento krok dokud je co odebírat.
Související články
Reference
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |