Čtverec

Z Multimediaexpo.cz

Verze z 27. 5. 2013, 09:56 (zobrazit zdroj) Sysop (diskuse | příspěvky) m (1 revizi) ← Porovnání se starší verzí		Verze z 2. 10. 2017, 15:42 (zobrazit zdroj) Sysop (diskuse | příspěvky) (+ Fotografie) Porovnání s novější verzí →
Řádka 12:		Řádka 12:
	== Vzorce ==		== Vzorce ==
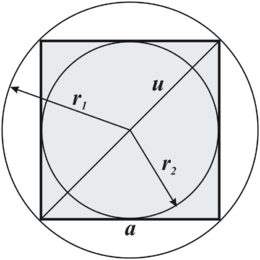
-	[[Soubor:Ctverec.png|right|250px|Čtverec s uhlopříčkou, vepsanou a opsanou kružnicí]]	+	[[Soubor:Ctverec-2006.png|thumb|260px|Čtverec s uhlopříčkou, vepsanou a opsanou kružnicí]]
	Pomocí délky strany čtverce <math>a</math> lze vyjádřit		Pomocí délky strany čtverce <math>a</math> lze vyjádřit
	* [[obvod]]		* [[obvod]]
Řádka 32:		Řádka 32:
	* [[Kružnice opsaná]]		* [[Kružnice opsaná]]
	* [[Kružnice vepsaná]]		* [[Kružnice vepsaná]]
		+
	{{Článek z Wikipedie}}		{{Článek z Wikipedie}}
	[[Kategorie:Mnohoúhelníky]]		[[Kategorie:Mnohoúhelníky]]

---

Verze z 2. 10. 2017, 15:42

V geometrii je čtverec pravidelný čtyřúhelník – rovinný útvar ohraničený čtyřmi úsečkami (stranami) stejné délky. Sousední strany spolu svírají pravý úhel. Čtverec lze také považovat za zvláštní případ obdélníku nebo kosočtverce - je to rovnoběžník. Přeneseně má čtverec někdy význam druhé mocniny, protože obsah čtverce je právě druhá mocnina délky jeho strany, například čtverec vzdálenosti čteme jako druhá mocnina vzdálenosti.

Vlastnosti

• Úhlopříčky čtverce se navzájem půlí.
• Úhlopříčky čtverce půlí jeho úhly.
• Úhlopříčky čtverce jsou navzájem kolmé.
• Protilehlé strany čtverce jsou rovnoběžné a stejně velké.
• Všechny čtyři úhly čtverce jsou stejně velké (Velikost každého úhlu je 360/4=90°, každý úhel čtverce je tedy pravý).
• Úhlopříčky čtverce jsou stejně velké.

Vzorce

Pomocí délky strany čtverce <math>a</math> lze vyjádřit

• obvod

<math> \ o = 4a</math>

• obsah

<math> \ S=a^2</math>

• délka úhlopříčky

<math>u=a\sqrt{2}</math>

• poloměr kružnice opsané

<math>r_1=\frac{u}{2}</math>

• poloměr kružnice vepsané

<math>r_2=\frac{a}{2}</math>

Související články

• Geometrický útvar
• Rovnoběžník
• Čtyřúhelník
• Obdélník
• Kružnice opsaná
• Kružnice vepsaná

Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010
Informace o článku. Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. Tento text je dostupný za podmínek Creative Commons 3.0 Unported – creativecommons.org. Originální článek na české Wikipedii