The final launch of the Allmultimedia.org will take place on February 27, 2026
(shortly after the 2026 Winter Olympics).
Meneláova věta
Z Multimediaexpo.cz
m (Nahrazení textu „<math>“ textem „<big>\(“) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| Řádka 5: | Řádka 5: | ||
== Znění Meneláovy věty == | == Znění Meneláovy věty == | ||
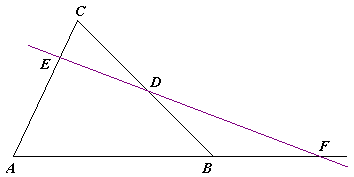
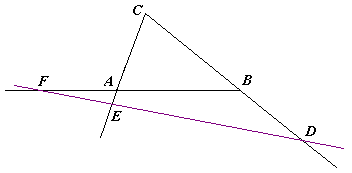
Máme-li dány [[bod]]y A,B a C, které tvoří [[trojúhelník]] ABC, a jiné body D, E a F, které leží na [[přímka|přímkách]] BC, AC a AB, pak body D, E a F leží na přímce právě tehdy, když platí | Máme-li dány [[bod]]y A,B a C, které tvoří [[trojúhelník]] ABC, a jiné body D, E a F, které leží na [[přímka|přímkách]] BC, AC a AB, pak body D, E a F leží na přímce právě tehdy, když platí | ||
| - | :<big>\(\frac{AF}{FB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA} = 1</ | + | :<big>\(\frac{AF}{FB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA} = 1\)</big> |
V tomto výrazu uvažujeme délky [[úsečka|úseček]] se znaménkem, které je dáno tím, nacházejí-li se body D, E a F uvnitř patřičných úseček, nebo vně. Například podíl AF/FB je kladný právě tehdy, pokud bod F leží na úsečce AB. | V tomto výrazu uvažujeme délky [[úsečka|úseček]] se znaménkem, které je dáno tím, nacházejí-li se body D, E a F uvnitř patřičných úseček, nebo vně. Například podíl AF/FB je kladný právě tehdy, pokud bod F leží na úsečce AB. | ||
| Řádka 16: | Řádka 16: | ||
Spustíme [[kolmice]] a, b a c z bodů A, B a C na přímku DEF. Z [[podobnost trojúhelníků|podobnosti trojúhelníků]] plyne, že | Spustíme [[kolmice]] a, b a c z bodů A, B a C na přímku DEF. Z [[podobnost trojúhelníků|podobnosti trojúhelníků]] plyne, že | ||
| - | :<big>\(\frac{|AF|}{|BF|}=\frac{a}{b}</ | + | :<big>\(\frac{|AF|}{|BF|}=\frac{a}{b}\)</big> |
| - | :<big>\(\frac{|BD|}{|CD|}=\frac{b}{c}</ | + | :<big>\(\frac{|BD|}{|CD|}=\frac{b}{c}\)</big> |
| - | :<big>\(\frac{|CE|}{|AE|}=\frac{c}{a}</ | + | :<big>\(\frac{|CE|}{|AE|}=\frac{c}{a}\)</big> |
tedy | tedy | ||
| - | :<big>\(\left|\frac{AF}{FB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA}\right| = \left|\frac{abc}{abc}\right|= 1</ | + | :<big>\(\left|\frac{AF}{FB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA}\right| = \left|\frac{abc}{abc}\right|= 1\)</big> |
Ještě zbývá dokázat, že pokud by body na přímce neležely, pak rovnost neplatí. Uvažujme bod X na přímce AB, který je různý od bodu F. Označme AF, AX a AB po řadě jako n, n', s. Předpokládejme, že rovnost platí i pro X. Pak platí | Ještě zbývá dokázat, že pokud by body na přímce neležely, pak rovnost neplatí. Uvažujme bod X na přímce AB, který je různý od bodu F. Označme AF, AX a AB po řadě jako n, n', s. Předpokládejme, že rovnost platí i pro X. Pak platí | ||
| - | :<big>\(\frac{AF}{FB} = \frac{AX}{XB},</ | + | :<big>\(\frac{AF}{FB} = \frac{AX}{XB},\)</big> |
neboli | neboli | ||
| - | :<big>\(\frac{n}{s-n} =\frac{n'}{s-n'},</ | + | :<big>\(\frac{n}{s-n} =\frac{n'}{s-n'},\)</big> |
| - | odkud uvedením na společného jmenovatele a zjednodušením dostaneme <big>\(n=n'</ | + | odkud uvedením na společného jmenovatele a zjednodušením dostaneme <big>\(n=n'\)</big>. Tedy <big>\(F=X\)</big>, čímž je důkaz hotov. |
== Externí odkazy == | == Externí odkazy == | ||
Aktuální verze z 14. 8. 2022, 14:52
Meneláova věta je tvrzení o trojúhelnících tradičně připisované starořeckému matematikovi Meneláovi Alexandrijskému. Je podobné Cévově větě.
Znění Meneláovy věty
Máme-li dány body A,B a C, které tvoří trojúhelník ABC, a jiné body D, E a F, které leží na přímkách BC, AC a AB, pak body D, E a F leží na přímce právě tehdy, když platí
- \(\frac{AF}{FB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA} = 1\)
V tomto výrazu uvažujeme délky úseček se znaménkem, které je dáno tím, nacházejí-li se body D, E a F uvnitř patřičných úseček, nebo vně. Například podíl AF/FB je kladný právě tehdy, pokud bod F leží na úsečce AB.
Důkaz
Nejdříve ověříme znaménko levé strany a ukážeme, že musí být vždy záporné. To plyne z toho, že přímka buď trojúhelník neprotne vůbec, nebo jej protne právě ve dvou bodech (viz Paschův axiom). Na levé straně je tedy lichý počet záporných zlomků a jejich součin bude vždy záporný.
Spustíme kolmice a, b a c z bodů A, B a C na přímku DEF. Z podobnosti trojúhelníků plyne, že
- \(\frac{|AF|}{|BF|}=\frac{a}{b}\)
- \(\frac{|BD|}{|CD|}=\frac{b}{c}\)
- \(\frac{|CE|}{|AE|}=\frac{c}{a}\)
tedy
- \(\left|\frac{AF}{FB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA}\right| = \left|\frac{abc}{abc}\right|= 1\)
Ještě zbývá dokázat, že pokud by body na přímce neležely, pak rovnost neplatí. Uvažujme bod X na přímce AB, který je různý od bodu F. Označme AF, AX a AB po řadě jako n, n', s. Předpokládejme, že rovnost platí i pro X. Pak platí
- \(\frac{AF}{FB} = \frac{AX}{XB},\)
neboli
- \(\frac{n}{s-n} =\frac{n'}{s-n'},\)
odkud uvedením na společného jmenovatele a zjednodušením dostaneme \(n=n'\). Tedy \(F=X\), čímž je důkaz hotov.
Externí odkazy
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |