Naše návštěvnost dne 25. února 2026 byla — 484 927 unikátních návštěvníků !!
Podgraf
Z Multimediaexpo.cz
m (Nahrazení textu „<math>“ textem „<big>\(“) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| Řádka 2: | Řádka 2: | ||
Termín '''podgraf''' se v [[teorie grafů|teorii grafů]] používá jako jistá obdoba pojmu [[podmnožina]]. | Termín '''podgraf''' se v [[teorie grafů|teorii grafů]] používá jako jistá obdoba pojmu [[podmnožina]]. | ||
| - | Graf <big>\(H=(V_H, E_H)</ | + | Graf <big>\(H=(V_H, E_H)\)</big> je ''podgraf'' [[graf (teorie grafů)|grafu]] <big>\(G=(V_G, E_G)\)</big>, jestliže platí následující podmínky: |
| - | # <big>\(V_H \subseteq V_G</ | + | # <big>\(V_H \subseteq V_G\)</big> |
| - | # <big>\(E_H \subseteq E_G</ | + | # <big>\(E_H \subseteq E_G\)</big> |
| - | # Hrany grafu <big>\(H</ | + | # Hrany grafu <big>\(H\)</big> mají oba vrcholy v <big>\(H\)</big>. |
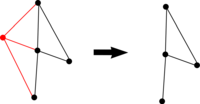
Jinými slovy, podgraf vznikne vymazáním některých vrcholů původního grafu, všech hran do těchto vrcholů zasahujících a případně některých dalších hran. | Jinými slovy, podgraf vznikne vymazáním některých vrcholů původního grafu, všech hran do těchto vrcholů zasahujících a případně některých dalších hran. | ||
== Indukovaný podgraf == | == Indukovaný podgraf == | ||
[[Soubor:Induced subgraph.png|thumb|200px|Původní graf a jeho indukovaný podgraf]] | [[Soubor:Induced subgraph.png|thumb|200px|Původní graf a jeho indukovaný podgraf]] | ||
| - | Graf H je ''indukovaný podgraf'' (též ''plný podgraf'') grafu G, jestli že je podgrafem G a pro každé dva vrcholy u, v grafu H plati: <big>\( (u, v) \in E_G \rightarrow (u,v) \in E_H</ | + | Graf H je ''indukovaný podgraf'' (též ''plný podgraf'') grafu G, jestli že je podgrafem G a pro každé dva vrcholy u, v grafu H plati: <big>\( (u, v) \in E_G \rightarrow (u,v) \in E_H\)</big>. |
Indukovaný podgraf vznikne vymazáním některých vrcholů a ''pouze'' těch hran, které do vymazaných vrcholů zasahují. | Indukovaný podgraf vznikne vymazáním některých vrcholů a ''pouze'' těch hran, které do vymazaných vrcholů zasahují. | ||
== Faktor == | == Faktor == | ||
| - | Podgraf H je faktor grafu G, jestliže množina vrcholů grafu H je totožná s množinou vrcholů grafu G, <big>\(V_H = V_G</ | + | Podgraf H je faktor grafu G, jestliže množina vrcholů grafu H je totožná s množinou vrcholů grafu G, <big>\(V_H = V_G\)</big>. Faktor též nazýváme '''hranovým podgrafem'''. |
== Kostra == | == Kostra == | ||
Aktuální verze z 14. 8. 2022, 14:53
Termín podgraf se v teorii grafů používá jako jistá obdoba pojmu podmnožina.
Graf \(H=(V_H, E_H)\) je podgraf grafu \(G=(V_G, E_G)\), jestliže platí následující podmínky:
- \(V_H \subseteq V_G\)
- \(E_H \subseteq E_G\)
- Hrany grafu \(H\) mají oba vrcholy v \(H\).
Jinými slovy, podgraf vznikne vymazáním některých vrcholů původního grafu, všech hran do těchto vrcholů zasahujících a případně některých dalších hran.
Obsah |
Indukovaný podgraf
Graf H je indukovaný podgraf (též plný podgraf) grafu G, jestli že je podgrafem G a pro každé dva vrcholy u, v grafu H plati: \( (u, v) \in E_G \rightarrow (u,v) \in E_H\).
Indukovaný podgraf vznikne vymazáním některých vrcholů a pouze těch hran, které do vymazaných vrcholů zasahují.
Faktor
Podgraf H je faktor grafu G, jestliže množina vrcholů grafu H je totožná s množinou vrcholů grafu G, \(V_H = V_G\). Faktor též nazýváme hranovým podgrafem.
Kostra
- Podrobnější informace naleznete v článku: Kostra grafu.
Kostra grafu G je takový jeho faktor, který neobsahuje kružnice. Ovšem musí být zachovány existence cest v grafu. Tzn. musí být zachován počet komponent grafu (počet souvislých částí grafu).
Klika
- Podrobnější informace naleznete v článku: Klika (teorie grafů).
Klikou grafu nazýváme takový podgraf, který je úplný. Nalezení kliky dané velikosti je známým NP-úplným problémem.
Související články
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |