Kružnice devíti bodů
Z Multimediaexpo.cz
m (1 revizi) |
(+ Nový článek) |
||
| Řádka 1: | Řádka 1: | ||
| - | + | [[Soubor:Nine-point circle.png|thumb|230px|Kružnice devíti bodů]] | |
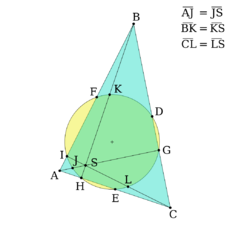
| + | [[Soubor:Circ9pnt3.png|thumb|230px|Kružnice devíti bodů se dotýká kružnice vepsané a kružnic připsaných]] | ||
| + | '''Kružnice devíti bodů''' se nazývá taková [[kružnice]] [[trojúhelník]]a, na níž leží jeho následující body: | ||
| + | *středy stran | ||
| + | *paty [[Trojúhelník#Výšky, těžnice a střední příčky|výšek]] | ||
| + | *středy spojnic vrcholů s ortocentrem (ortocentrum = společný bod výšek trojúhelníka) | ||
| + | Kružnice devíti bodů se nazývá též '''Feuerbachova kružnice''', protože německý matematik [[Karl Wilhelm Feuerbach]] byl prvním, kdo dokázal, že se kružnice devíti bodů dotýká [[kružnice vepsaná|kružnice vepsané]] a [[kružnice připsaná|kružnic připsaných]]. | ||
| + | |||
| + | Kružnice devíti bodů je [[stejnolehlost|stejnolehlým]] obrazem [[kružnice opsaná|kružnice opsané]] se středem stejnolehlosti v [[Trojúhelník#Výšky, těžnice a střední příčky|těžišti]] trojúhelníka a koeficientem κ = - 0,5. Z toho plyne, že její střed leží na [[Eulerova přímka|Eulerově přímce]] ve středu úsečky, spojující [[Výška (geometrie)|ortocentrum]] se středem kružnice opsané. Její poloměr je polovinou poloměru kružnice opsané. | ||
| + | |||
| + | == Související články == | ||
| + | * [[Eulerova přímka]] | ||
| + | * [[Kružnice]] | ||
| + | * [[Trojúhelník]] | ||
| + | |||
| + | |||
| + | {{Článek z Wikipedie}} | ||
[[Kategorie:Kružnice]] | [[Kategorie:Kružnice]] | ||
[[Kategorie:Trojúhelník]] | [[Kategorie:Trojúhelník]] | ||
Aktuální verze z 11. 10. 2015, 13:02
Kružnice devíti bodů se nazývá taková kružnice trojúhelníka, na níž leží jeho následující body:
- středy stran
- paty výšek
- středy spojnic vrcholů s ortocentrem (ortocentrum = společný bod výšek trojúhelníka)
Kružnice devíti bodů se nazývá též Feuerbachova kružnice, protože německý matematik Karl Wilhelm Feuerbach byl prvním, kdo dokázal, že se kružnice devíti bodů dotýká kružnice vepsané a kružnic připsaných.
Kružnice devíti bodů je stejnolehlým obrazem kružnice opsané se středem stejnolehlosti v těžišti trojúhelníka a koeficientem κ = - 0,5. Z toho plyne, že její střed leží na Eulerově přímce ve středu úsečky, spojující ortocentrum se středem kružnice opsané. Její poloměr je polovinou poloměru kružnice opsané.
Související články
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |