Hyperbolická geometrie

Z Multimediaexpo.cz

Verze z 24. 5. 2014, 16:07 (zobrazit zdroj) Sysop (diskuse | příspěvky) m (1 revizi) ← Porovnání se starší verzí		Aktuální verze z 11. 8. 2014, 19:03 (zobrazit zdroj) Sysop (diskuse | příspěvky) (+ Masivní vylepšení)
Řádka 1:		Řádka 1:
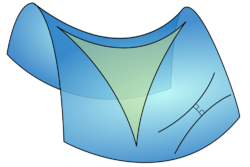
-	{{Wikipedia-cs|Hyperbolická geometrie|700}}	+	[[Soubor:Hyperbolic triangle.png|thumb|250px|Trojúhelník a dvě rovnoběžky na hyperbolickém paraboloidu]]
		+	V [[matematika|matematice]] je '''hyperbolická geometrie''' (nebo také '''Lobačevského geometrie''') [[Neeukleidovská geometrie|neeukleidovskou geometrií]], což znamená, že nesplňuje pátý [[Eukleidův postulát]] (o [[rovnoběžka|rovnoběžkách]]). Ten říká, že v dvourozměrném prostoru pro přímku ''l'' a bod ''P'' ležící mimo ni existuje právě jedna přímka, která bodem ''P'' prochází a zároveň neprotíná ''l''; neboli je rovnoběžná s ''l''. V hyperbolické geometrii takové přímky existují alespoň dvě, takže tento postulát zde neplatí.
		+	Hyperbolická geometrie se dá zkonstruovat axiomaticky, ale je také možné udělat její model zadáním jisté metriky na hladké varietě. Existence hyperbolické geometrie implikuje nezávislost postulátu o rovnoběžkách na ostatních Eukleidových postulátech. Lokálně se dá hyperbolická geometrie modelovat na části plochy, která má zápornou [[Gaussova křivost|Gaussovu křivost]], např. jednodílného [[hyperboloid]]u nebo [[hyperbolický paraboloid|hyperbolického paraboloidu]].
		+
		+	Charakteristickou vlastností hyperbolické geometrie je, že součet vnitřních [[úhel|úhlů]] každého [[trojúhelník]]u v této geometrii je menší než 180[[Stupeň (úhel)|°]]. Součet vnitřních úhlů trojúhelníka může být libovolně malý.
		+
		+	== Externí odkazy ==
		+	* Vladimir Bulatov, [http://bulatov.org/math/1001/ Conformal Models of the Hyperbolic Geometry], Modely a animace transformací hyperbolické roviny
		+
		+
		+	{{commonscat|Hyperbolic geometry}}{{Článek z Wikipedie}}
	[[Kategorie:Geometrie]]		[[Kategorie:Geometrie]]

---

Aktuální verze z 11. 8. 2014, 19:03

V matematice je hyperbolická geometrie (nebo také Lobačevského geometrie) neeukleidovskou geometrií, což znamená, že nesplňuje pátý Eukleidův postulát (o rovnoběžkách). Ten říká, že v dvourozměrném prostoru pro přímku l a bod P ležící mimo ni existuje právě jedna přímka, která bodem P prochází a zároveň neprotíná l; neboli je rovnoběžná s l. V hyperbolické geometrii takové přímky existují alespoň dvě, takže tento postulát zde neplatí.

Hyperbolická geometrie se dá zkonstruovat axiomaticky, ale je také možné udělat její model zadáním jisté metriky na hladké varietě. Existence hyperbolické geometrie implikuje nezávislost postulátu o rovnoběžkách na ostatních Eukleidových postulátech. Lokálně se dá hyperbolická geometrie modelovat na části plochy, která má zápornou Gaussovu křivost, např. jednodílného hyperboloidu nebo hyperbolického paraboloidu.

Charakteristickou vlastností hyperbolické geometrie je, že součet vnitřních úhlů každého trojúhelníku v této geometrii je menší než 180°. Součet vnitřních úhlů trojúhelníka může být libovolně malý.

Externí odkazy

• Vladimir Bulatov, Conformal Models of the Hyperbolic Geometry, Modely a animace transformací hyperbolické roviny

Commons nabízí fotografie, obrázky a videa k tématu Hyperbolická geometrie

Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010
Informace o článku. Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. Tento text je dostupný za podmínek Creative Commons 3.0 Unported – creativecommons.org. Originální článek na české Wikipedii