V sobotu 2. listopadu proběhla mohutná oslava naší plnoletosti !!
Multimediaexpo.cz je již 18 let na českém internetu !!
V tiskové zprávě k 18. narozeninám brzy najdete nové a zásadní informace.
Multimediaexpo.cz je již 18 let na českém internetu !!
V tiskové zprávě k 18. narozeninám brzy najdete nové a zásadní informace.
Mocninná funkce
Z Multimediaexpo.cz
(Rozdíly mezi verzemi)
(+ Nový článek) |
m (Nahrazení textu „<math>“ textem „<big>\(“) |
||
| Řádka 1: | Řádka 1: | ||
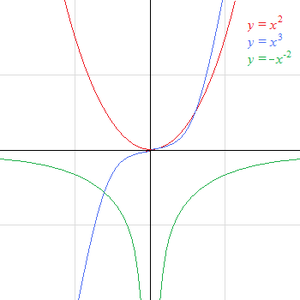
[[Soubor:Funkcie mocniny2.png|thumb|300px|Grafy mocninných funkcí pro exponent 2, 3 a -2]] | [[Soubor:Funkcie mocniny2.png|thumb|300px|Grafy mocninných funkcí pro exponent 2, 3 a -2]] | ||
'''Mocninná funkce''' je [[Elementární funkce|elementární matematická funkce]] tvaru | '''Mocninná funkce''' je [[Elementární funkce|elementární matematická funkce]] tvaru | ||
| - | :< | + | :<big>\(f\colon x \mapsto a x^r \qquad a,r \in \mathbb{R},</math> |
| - | kde < | + | kde <big>\(a</math> a <big>\(r</math> jsou [[konstanta|konstanty]] a <big>\(x</math> je proměnná. |
== Definiční obor == | == Definiční obor == | ||
| - | Definiční obor závisí na exponentu < | + | Definiční obor závisí na exponentu <big>\(r</math>. |
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| - | ! !! < | + | ! !! <big>\(r > 0</math> !! <big>\(r < 0</math> |
|- | |- | ||
| - | | < | + | | <big>\(r \in \mathbb{Z}</math> || style="text-align:center" | <big>\(\mathbb{R}</math> || style="text-align:center" | <big>\(\mathbb{R}\setminus\{0\}</math> |
|- | |- | ||
| - | | < | + | | <big>\(r \notin \mathbb{Z}</math> || style="text-align:center" | <big>\(\mathbb{R}^+_0</math> || style="text-align:center" | <big>\(\mathbb{R}^+</math> |
|} | |} | ||
== Obor hodnot == | == Obor hodnot == | ||
| - | Obor hodnot závisí na konstantě < | + | Obor hodnot závisí na konstantě <big>\(a</math> a exponentu <big>\(r</math>. |
{| class="wikitable" | {| class="wikitable" | ||
| - | ! || colspan="2" | < | + | ! || colspan="2" | <big>\(r > 0</math> || colspan="2" | <big>\(r < 0</math> |
|- | |- | ||
| - | ! !! < | + | ! !! <big>\(r</math> sudé <br /> nebo <big>\(\notin \mathbb{Z}</math> !! <big>\(r</math> liché !! <big>\(r</math> sudé <br /> nebo <big>\(\notin \mathbb{Z}</math> !! <big>\(r</math> liché |
|- | |- | ||
| - | | < | + | | <big>\(a > 0</math> || style="text-align:center" | <big>\(\mathbb{R}^+_0</math> || style="text-align:center" | <big>\(\mathbb{R}</math> || style="text-align:center" | <big>\(\mathbb{R}^+</math> || style="text-align:center" | <big>\(\mathbb{R}\setminus\{0\}</math> |
|- | |- | ||
| - | | < | + | | <big>\(a < 0</math> || style="text-align:center" | <big>\(\mathbb{R}^-_0</math> || style="text-align:center" | <big>\(\mathbb{R}</math> || style="text-align:center" | <big>\(\mathbb{R}^-</math> || style="text-align:center" | <big>\(\mathbb{R}\setminus\{0\}</math> |
|} | |} | ||
Verze z 14. 8. 2022, 14:49
Mocninná funkce je elementární matematická funkce tvaru
- \(f\colon x \mapsto a x^r \qquad a,r \in \mathbb{R},</math>
kde \(a</math> a \(r</math> jsou konstanty a \(x</math> je proměnná.
Definiční obor
Definiční obor závisí na exponentu \(r</math>.
| \(r > 0</math> | \(r < 0</math> | |
|---|---|---|
| \(r \in \mathbb{Z}</math> | \(\mathbb{R}</math> | \(\mathbb{R}\setminus\{0\}</math> |
| \(r \notin \mathbb{Z}</math> | \(\mathbb{R}^+_0</math> | \(\mathbb{R}^+</math> |
Obor hodnot
Obor hodnot závisí na konstantě \(a</math> a exponentu \(r</math>.
| \(r > 0</math> | \(r < 0</math> | |||
|---|---|---|---|---|
| \(r</math> sudé nebo \(\notin \mathbb{Z}</math> | \(r</math> liché | \(r</math> sudé nebo \(\notin \mathbb{Z}</math> | \(r</math> liché | |
| \(a > 0</math> | \(\mathbb{R}^+_0</math> | \(\mathbb{R}</math> | \(\mathbb{R}^+</math> | \(\mathbb{R}\setminus\{0\}</math> |
| \(a < 0</math> | \(\mathbb{R}^-_0</math> | \(\mathbb{R}</math> | \(\mathbb{R}^-</math> | \(\mathbb{R}\setminus\{0\}</math> |
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |