The English encyclopedia Allmultimedia.org will be launched in two phases.
The final launch of the Allmultimedia.org will take place on February 27, 2026
(shortly after the 2026 Winter Olympics).
The final launch of the Allmultimedia.org will take place on February 27, 2026
(shortly after the 2026 Winter Olympics).
Tětiva (geometrie)
Z Multimediaexpo.cz
(Rozdíly mezi verzemi)
(+ Masivní vylepšení) |
m (Nahrazení textu „<math>“ textem „<big>\(“) |
||
| Řádka 2: | Řádka 2: | ||
'''Tětiva''' je [[úsečka]] spojující dva body na [[kružnice|kružnici]]. Tětiva procházející středem je ze všech nejdelší a nazývá se [[Průměr (geometrie)|průměrem]] [[kružnice]]. | '''Tětiva''' je [[úsečka]] spojující dva body na [[kružnice|kružnici]]. Tětiva procházející středem je ze všech nejdelší a nazývá se [[Průměr (geometrie)|průměrem]] [[kružnice]]. | ||
| - | Dělí [[kruh]] na dvě [[kruhová úseč|kruhové úseče]]. Je příslušná konvexnímu [[středový úhel|středovému úhlu]] < | + | Dělí [[kruh]] na dvě [[kruhová úseč|kruhové úseče]]. Je příslušná konvexnímu [[středový úhel|středovému úhlu]] <big>\(\alpha\,\!</math>. Pro každou tětivu platí, že její osa prochází středem dané kružnice. |
== Délka tětivy == | == Délka tětivy == | ||
| - | Délka tětivy je < | + | Délka tětivy je <big>\(2\cdot r\cdot \sin{(\frac{\alpha}{2})}</math> kde <big>\(r\,\!</math> je poloměr kružnice<br /> |
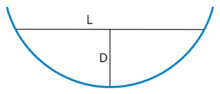
| - | nebo < | + | nebo <big>\(2\sqrt{r^2-(r-D)^2}=2\sqrt{r^2-(r^2-2rD+D^2)}=2\sqrt{2rD-D^2}=2\sqrt{D\cdot(2r-D)}</math> |
== Související články == | == Související články == | ||
Verze z 14. 8. 2022, 14:50
Tětiva je úsečka spojující dva body na kružnici. Tětiva procházející středem je ze všech nejdelší a nazývá se průměrem kružnice.
Dělí kruh na dvě kruhové úseče. Je příslušná konvexnímu středovému úhlu \(\alpha\,\!</math>. Pro každou tětivu platí, že její osa prochází středem dané kružnice.
Délka tětivy
Délka tětivy je \(2\cdot r\cdot \sin{(\frac{\alpha}{2})}</math> kde \(r\,\!</math> je poloměr kružnice
nebo \(2\sqrt{r^2-(r-D)^2}=2\sqrt{r^2-(r^2-2rD+D^2)}=2\sqrt{2rD-D^2}=2\sqrt{D\cdot(2r-D)}</math>
Související články
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |