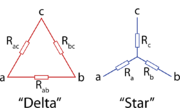
Přepočet hvězda trojúhelník

Z Multimediaexpo.cz

(Rozdíly mezi verzemi)

Aktuální verze z 14. 8. 2022, 14:53

Transkonfigurace – Pro odpory nebo v obvodu harmonického střídavého proudu impedance zapojené ve hvězdě platí, že je možno je nahradit ekvivalentním zapojením do trojúhelníku. Zapojení do trojúhelníku se v elektrotechnice někdy označuje také písmenem D, zapojení do hvězdy písmenem Y. Zapojení do trojúhelníku a zapojení do hvězdy jsou základním způsobem zapojení elektrických spotřebičů ve třífázové soustavě.

Zapojení impedancí do trojúhelníku lze nahradit zapojením vhodných hodnot do hvězdy a naopak. Pro náhradu zapojení do trojúhelníku zapojením do hvězdy platí:

\(Z_a = \frac{Z_{ab} \cdot Z_{ac}}{Z_{bc}+Z_{ac}+Z_{ab}}\)

\(Z_b = \frac{Z_{ab} \cdot Z_{bc}}{Z_{bc}+Z_{ac}+Z_{ab}}\)

\(Z_c = \frac{Z_{ac} \cdot Z_{bc}}{Z_{bc}+Z_{ac}+Z_{ab}}\)

Obráceně pro náhradu zapojení do hvězdy zapojením do trojúhelníku platí:

\(Z_{ab} = \frac{Z_a Z_b + Z_a Z_c + Z_b Z_c}{Z_c}\)

\(Z_{ac} = \frac{Z_a Z_b + Z_a Z_c + Z_b Z_c}{Z_b}\)

\(Z_{bc} = \frac{Z_a Z_b + Z_a Z_c + Z_b Z_c}{Z_a}\)

Odvození vztahů pro transfiguraci

Rovnice pro odvození přepočtu hvězdy na trojúhelník plynou ze srovnání hodnot impedancí při odpojení jednoho bodu. Rovnice pro odvození přepočtu trojúhelníku na hvězdu plynou ze srovnání hodnot admitancí při připojení dvou bodů na stejný potenciál (tj. zkratování dvou bodů).

Srovnání zapojení do hvězdy a do trojúhelníku

Nejčastějším případem v praxi je situace při zapojování spotřebičů ve třífázové soustavě, kdy jsou všechny odpory nebo impedance zapojované do hvězdy nebo do trojúhelníku stejné nebo téměř stejné. Při ekvivalentním zapojení podle výše uvedených přepočtů je výkonové namáhání prvků stejné, v trojúhelníku je vyšší napěťové namáhání prvků, ve hvězdě tečou vyšší proudy. U cívek nebo kondenzátorů zjišťujeme že energie v jednotlivých prvcích vychází stejně, takže změnou zapojení nic nezískáváme.

Při přepojení spotřebičů z hvězdy do trojúhelníku dochází ke zvýšní napětí na spotřebičích a tedy ke zvýšení výkonu, konkrétně ve třífázové soustavě u symetrického spotřebiče jde o zvýšení napětí na násobek odmocniny ze tří a výkonu na trojnásobek. Možností využívanou u elektrických motorů je připojení třífázového motoru na nižší napětí (např. 3 x 230V AC) při zapojení vinutí do trojúhelníku nebo na vyšší napětí (např. 3 x 400V AC) při zapojení vinutí do hvězdy.

Externí odkazy

Online kalkulátor transfigurace hvězda - trojúhelník

Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010
Informace o článku. Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. Tento text je dostupný za podmínek Creative Commons 3.0 Unported – creativecommons.org. Originální článek na české Wikipedii

@@ Řádka 5: / Řádka 5: @@
 Zapojení [[impedance|impedancí]] do trojúhelníku lze nahradit zapojením vhodných hodnot do hvězdy a naopak. Pro náhradu zapojení do trojúhelníku zapojením do hvězdy platí:
-<big>\(Z_a = \frac{Z_{ab} \cdot Z_{ac}}{Z_{bc}+Z_{ac}+Z_{ab}}</math>
+<big>\(Z_a = \frac{Z_{ab} \cdot Z_{ac}}{Z_{bc}+Z_{ac}+Z_{ab}}\)</big>
-<big>\(Z_b = \frac{Z_{ab} \cdot Z_{bc}}{Z_{bc}+Z_{ac}+Z_{ab}}</math>
+<big>\(Z_b = \frac{Z_{ab} \cdot Z_{bc}}{Z_{bc}+Z_{ac}+Z_{ab}}\)</big>
-<big>\(Z_c = \frac{Z_{ac} \cdot Z_{bc}}{Z_{bc}+Z_{ac}+Z_{ab}}</math>
+<big>\(Z_c = \frac{Z_{ac} \cdot Z_{bc}}{Z_{bc}+Z_{ac}+Z_{ab}}\)</big>
 Obráceně pro náhradu zapojení do hvězdy zapojením do trojúhelníku platí:
-<big>\(Z_{ab} = \frac{Z_a Z_b + Z_a Z_c + Z_b Z_c}{Z_c}</math>
+<big>\(Z_{ab} = \frac{Z_a Z_b + Z_a Z_c + Z_b Z_c}{Z_c}\)</big>
-<big>\(Z_{ac} = \frac{Z_a Z_b + Z_a Z_c + Z_b Z_c}{Z_b}</math>
+<big>\(Z_{ac} = \frac{Z_a Z_b + Z_a Z_c + Z_b Z_c}{Z_b}\)</big>
-<big>\(Z_{bc} = \frac{Z_a Z_b + Z_a Z_c + Z_b Z_c}{Z_a}</math>
+<big>\(Z_{bc} = \frac{Z_a Z_b + Z_a Z_c + Z_b Z_c}{Z_a}\)</big>
 == Odvození vztahů pro transfiguraci==