Rovina

Z Multimediaexpo.cz

Verze z 27. 12. 2023, 11:31; Sysop (diskuse | příspěvky)
(rozdíl) ← Starší verze | zobrazit aktuální verzi (rozdíl) | Novější verze → (rozdíl)


Rovina je v matematice dvourozměrný geometrický útvar, který si lze představit jako neomezenou dokonale rovnou plochu. Algebraicky vyjádřeno, jde o množinu bodů izomorfní s dvoudimenzionálním lineárním prostorem. Rovina může být určena třemi různými body, nebo přímkou a bodem, který leží mimo tuto přímku.

Obsah

Značení

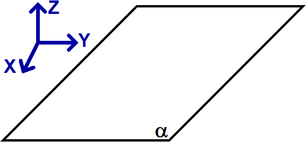
Rovina je buď plocha, na kterou se kreslí (nákresna), nebo se znázorňuje některým rovinným útvarem pomocí některého geometrických promítání. Rovina se označuje malým řeckým písmenem.

Znázornění:

Zobrazení roviny

Rovnice roviny

Rovina je množina bodů prostoru, které vyhovují tzv. rovnici roviny, která může být zadána v různých tvarech.

Obecná rovnice roviny

Obecná rovnice roviny má tvar

\(ax+by+cz+d=0\,\!\),

kde koeficienty \(a,\,b,\,c\,\!\) nejsou současně nulové a jsou to koeficienty normálového vektoru roviny (vektoru kolmého k rovině). Proměnné \(x,\,y,\,z\,\!\) jsou souřadnice bodu ležícího v rovině. V případě, že známe tři body \(K,\,L,\,M\) určující rovinu, obecnou rovnici roviny získáme takto: spočteme vektory \(\overrightarrow{KL}\) a \(\overrightarrow{KM}\), vypočítáme jejich Vektorový součin ze kterého získáme koeficienty \(a,\,b,\,c\,\!\) a napíšeme obecnou rovnici. Zbývající koeficient d získáme tak, že dosadíme souřadnice bodu K (nebo kteréhokoli jiného bodu ze zadání) do napsané rovnice.

Parametrické vyjádření roviny

Parametrické vyjádření roviny má například vektorový tvar \(X=A+t u + s v\,\!\), který se dá rozepsat dle složek takto:

\(x=A_1+t u_1+s v_1\,\!\)
\(y=A_2+t u_2+s v_2\,\!\)
\(z=A_3+t u_3+s v_3\,\!\),

kde \(s,\,t \in R\,\!\) a \(X\,\!\) je bod, který leží v rovině a vektory \(u\,\!\) a \(v\,\!\) jsou nekolineární vektory ležící v rovině, tzn. jsou to směrové vektory roviny.

Úseková rovnice roviny

Úsekovou rovnici roviny zapisujeme jako

\(\frac{x}{p} + \frac{y}{q} + \frac{z}{r} = 1\),

kde \(p,\,q,\,r\) vymezují úseky vyťaté rovinou na osách \(x,\,y,\,z\,\!\). Srovnáním úsekové a obecné rovnice dostáváme \(p = -\frac{d}{a},\,q = -\frac{d}{b},\,r = -\frac{d}{c}\,\!\).

Normálová rovnice roviny

Normálová rovnice roviny má tvar

\(x\cos\alpha + y\cos\beta + z\cos\gamma + p = 0\,\!\),

kde \(p\,\!\) je vzdálenost počátku souřadného systému od roviny, tj. délka normály od počátku souřadnicového systému do průsečíku s rovinou,
\(\cos\alpha,\,\cos\beta,\,\cos\gamma\,\!\) jsou směrové kosiny roviny,
\(\alpha,\,\beta,\,\gamma\,\!\) představují úhly, které svírají kladné souřadnicové poloosy s normálou roviny.
Normála je směrnice kolmá ve všech směrech k rovině.
Směrové kosiny lze vyjádřit z obecné rovnice jako

\(\cos\alpha = \frac{a}{\varepsilon\sqrt{a^2+b^2+c^2}}\)
\(\cos\beta = \frac{b}{\varepsilon\sqrt{a^2+b^2+c^2}}\)
\(\cos\gamma = \frac{c}{\varepsilon\sqrt{a^2+b^2+c^2}}\)

kde \(\varepsilon=1\,\!\) pro \({\operatorname{sgn}} (p) = -1\,\!\) a pro \(\varepsilon=-1\,\!\) pro \({\operatorname{sgn}} (p)=1\,\!\).

Rovinný řez

Rovinným řezem geometrického útvaru \(U\) rovinou \(\rho\) se nazývá průnik roviny \(\rho\) a útvaru \(U\). Rovinný řez plochy rovinou, ve které leží normála plochy, se nazývá normálovým řezem plochy.

Související články


Citováno z „http://ww.multimediaexpo.cz/mmecz/index.php/Rovina“