V sobotu 2. listopadu proběhla mohutná oslava naší plnoletosti !!
Multimediaexpo.cz je již 18 let na českém internetu !!
V tiskové zprávě k 18. narozeninám brzy najdete nové a zásadní informace.

Impedance

Z Multimediaexpo.cz

Verze z 15. 11. 2011, 23:08; Sysop (diskuse | příspěvky)
(rozdíl) ← Starší verze | zobrazit aktuální verzi (rozdíl) | Novější verze → (rozdíl)

Impedance je jednobran obsahující rezistory a akumulační prvky. Jde o komplexní veličinu (obsahuje reálnou a imaginární složku) popisující zdánlivý odpor součástky a fázový posuv napětí proti proudu při průchodu harmonického střídavého elektrického proudu dané frekvence. Podobně jako elektrický odpor charakterizuje vlastnosti prvku pro stejnosměrný proud, impedance charakterizuje vlastnosti prvku pro střídavý proud. Impedance je základní vlastností, kterou potřebujeme znát pro analýzu střídavých elektrických obvodů.

Obsah

Značení

Jelikož je impedance komplexní veličina, značí se jako vektor <math>\mathbf Z</math>. Jednotka impedance je shodná s jednotkou elektrického odporu a reaktance (induktance, kapacitance), kterou je ohm <math>\Omega</math>. Jde o poměr napětí a proudu. Na rozdíl od elektrického odporu, kde je napětí s proudem ve fázi, u impedance mohou být fázově posunuty.

Vyjádření impedance

Jde o poměr napětí a proudu, kde napětí i proud jsou fázory.

<math>\mathbf Z = \frac{\mathbf U}{\mathbf I} [\Omega; V, A]</math>

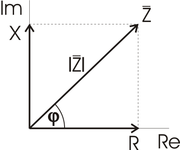
Protože je impedance komplexní veličina, má dvě složky, reálnou a imaginární. Reálnou složku vynášíme na reálnou osu v komplexní rovině a imaginární složku vynášíme na imaginární osu v komplexní rovině.

Impedance jako komplexní veličina

Z charakteristiky vidíme, že platí:

<math>\mathbf Z=R + jX =|\mathbf Z| cos\varphi + j|\mathbf Z|sin\varphi</math>

Polární zápis:

<math>\mathbf Z=|\mathbf Z|e^{j\varphi}</math>

Absolutní hodnotu impedance vypočteme užitím Pythagorovy věty:

<math>|\mathbf Z|=\sqrt{R^2+X^2}</math>

Převrácená hodnota impedance se nazývá admitance. Značí se Y a platí:

<math>\mathbf Z=\frac{1}{Y} [\Omega; S]</math>

Impedance přenosové trasy Každý elektrický (metalický) datový vodič má svůj vlastní odpor(R [Ohm], jelikož je to "drát" tak i indukčnost( L [H]), jeho izolace (dielektrikum) se projevuje kapacitou( C [F]), ale i ta má svůj odpor, vyjádřený svodou vodivostí(G [S]). Dohromady se tyto prvky vyjadřují impedancí danou vztahem:

<math>Zo=\sqrt{\frac {R + j \omega L}{G + j \omega C}}</math>

Vyjádříme-li si Zo ve složkovém tvaru Zo=alfa+j Beta , pak alfa je měrný útlum a Beta je měrný fázový posun. Zo má velice významné využití- např impedance u koaxálních kabelů. Impedance odporu: <math>Z = R\,\!</math> Impedance cívky: <math>Z = j \omega L\,\!</math> , kde L je indukčnost cívky a ω je úhlová frekvence Impedance kondenzátoru: <math>Z = \frac {1}{j \omega C}</math>, kde C je kapacita kondenzátoru a ω je úhlová frekvence Impedance závisí na frekvenci, protože <math>\omega = 2 \pi f\,\!</math>, kde f je frekvence.

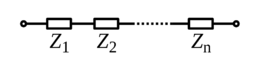
Spojování impedancí

Impedance se spojují stejně jako odpory, jen s tím rozdílem, že jsou to komplexní čísla.

Sériové spojování impedancí

Impedances in series.png

<math>\mathbf{Z} = \mathbf{Z}_1 + \mathbf{Z}_2 = (R_1 + R_2) + j(\Chi_1 + \Chi_2) \quad</math>

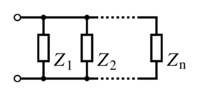
Paralelní spojování impedancí

Impedances in parallel.png

<math>\mathbf{Z} = \mathbf{Z}_1 \| \mathbf{Z}_2 = \left(\mathbf{Z}_1^{-1} + \mathbf{Z}_2^{-1}\right)^{-1} = {\mathbf{Z}_1 \mathbf{Z}_2 \over \mathbf{Z}_1 + \mathbf{Z}_2} \quad</math>

Měření impedancí

Při měření impedance musíme napájet obvod vždy střídavým sinusovým proudem, protože jinak bychom měřili pouze činnou složku impedance, tj. ohmický odpor.

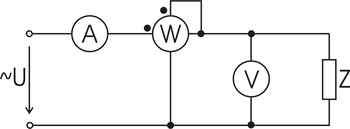
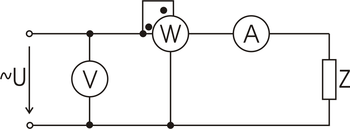
Měření voltmetrem, ampérmetrem a wattmetrem

Vztahy

Podíl efektivních hodnot napětí a proudu nám dá absolutní hodnotu impedance.

<math>|\mathbf{Z}|=\frac{U}{I}</math>

Velikost fázového posunu

<math>\ P=UIcos\varphi</math>

Velikost činného odporu

<math>P=RI^2=>R=\frac{P}{I^2}</math>

Velikost reaktance

<math>X=|\mathbf{Z}|sin\varphi</math>

Velikost vlastní indukčnosti (pro induktivní charakter zátěže)

<math>L=\frac{X}{2\pi f}</math>

Velikost elektrické kapacity (pro kapacitní charakter zátěže)

<math>\ C=\frac {1}{2\pi f X}</math>

Hraniční impedance

Velikost hraniční impedance určuje, zda je vhodnější použít zapojení pro malé nebo pro velké impedance.

<math>|\mathbf{Z_h}|\approx \sqrt{(R_A + R_{WP}) \frac{R_VR_{WN}}{R_V + R_{WN}}}</math>
<math>R_A</math> - vnitřní odpor ampérmetru
<math>R_V</math> - vnitřní odpor voltmetru
<math>R_{WP}</math> - vnitřní odpor proudové cívky wattmetru
<math>R_{WN}</math> - vnitřní odpor napěťové cívky wattmetru

Tato metoda není přesná, protože velikosti jednotlivých složek zjišťujeme více výpočty. Používá se pouze pro orientační měření.

Zapojení pro měření malých impedancí

Zapojení pro měření malých impedancí

Zapojení pro měření velkých impedancí

Zapojení pro měření velkých impedancí

Metoda tří ampérmetrů

Neznámou impdanci <math>Z_x</math> zapojíme paralelně se známým odporovým normálem <math>R_N</math>. Třemi ampérmetry měříme efektivní hodnoty proudů v jednotlivých větvích i proud celkový. Metoda tří ampérmetrů je nejpřesnější, jsou-li proudy I_R a I_Z stejně velké a fázový posun způsobený měřenou impedancí je velký. 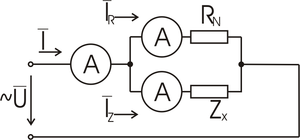Metoda tří ampérmetrů Velikost napětí

<math>\mathbf{U}=\mathbf{Z_x}\mathbf{I_Z}=R_N\mathbf{I_R}</math>

Velikost absolutní hodnoty impedance

<math>\mathbf{|Z_x|}=\frac{RI_R}{I_Z}</math>

Podle prvního Kirchhoffova zákona platí

<math>\mathbf{I}=\mathbf{I_R}+\mathbf{I_Z}</math>

Podle fázorového diagramu platí pro úhel <math>\varphi'</math> kosinová věta

<math>I^2=I_Z^2 + I_R^2 - 2I_RI_Zcos\varphi'</math>

Pro <math>cos\varphi'</math> platí

<math>cos\varphi'=-\frac{I^2-I_Z^2-I_R^2}{2I_RI_Z}</math>

Pro úhel <math>\varphi</math> platí

<math>\ \varphi=180 - \varphi'</math>

Pro <math>cos\varphi</math> platí

<math>\ cos\varphi=-cos\varphi'</math>
<math>cos\varphi=\frac{I^2-I_Z^2-I_R^2}{2I_RI_Z}</math>

Jednotlivé složky impedance budou mít velikost

<math>\ R_x=\mathbf|Z|cos\varphi</math>
<math>\ X_x=\mathbf|Z|sin\varphi</math>

Pro činný výkon na zátěži platí

<math>P=U_ZI_Zcos\varphi=R_NI_RI_Z\frac{I^2-I_Z^2-I_R^2}{2I_RI_Z}=\frac{R_N}{2}(I^2-I_R^2-I_Z^2)</math>

Metoda tří voltmetrů

Měřená impedance <math>Z_x</math> je zapojena v sérii s odporovým normálem <math>R_N</math>. Pomocí tří voltmetrů měříme efektivní hodnoty úbytků napětí na normálu, na měřené impedanci a napětí celkové. 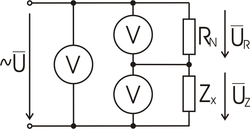Metoda tří voltmetrů Podle fázorového diagramu platí pro úhel <math>\varphi'</math> kosinová věta

<math>U^2=U_Z^2 + U_R^2 - 2U_RU_Zcos\varphi'</math>

Pro <math>cos\varphi'</math> platí

<math>cos\varphi'=-\frac{U^2-U_Z^2-U_R^2}{2U_RU_Z}</math>

Pro úhel <math>\varphi</math> platí

<math>\ \varphi=180 - \varphi'</math>

Pro <math>cos\varphi</math> platí

<math>\ cos\varphi=-cos\varphi'</math>
<math>cos\varphi=\frac{U^2-U_Z^2-U_R^2}{2U_RU_Z}</math>

Jednotlivé složky impedance budou mít velikost

<math>\ R_x=\mathbf|Z|cos\varphi</math>
<math>\ X_x=\mathbf|Z|sin\varphi</math>

Pro činný výkon na zátěži platí

<math>P=U_ZI_Zcos\varphi=\frac{U_ZU_R}{R_N}\frac{U^2-U_Z^2-U_R^2}{2U_RU_Z}=\frac{U^2-U_R^2-U_Z^2}{2R_N}</math>

Hraniční impedance

Zda máme použít k měření impedance metodu tří ampérmetrů nebo voltmetrů rozhodne hodnota hraniční impedance. Pro určení její velikosti platí vztah.

<math>\mathbf{Z_h}\approx \sqrt{R_AR_V}</math>
<math>R_A</math> - vnitřní odpor ampérmetrů
<math>R_V</math> - vnitřní odpor voltmetrů

Je-li <math>|\mathbf{Z_x}|<|\mathbf{Z_h}|</math>, je pro měření vhodnější metoda tří voltmetrů, pro <math>|\mathbf{Z_x}|>|\mathbf{Z_h}|</math> je pro měření vhodnější metoda tří ampérmetrů.

Obecný můstek

Obecný můstek

Jde o obdobu Wheatstoneova můstku pro měření odporů. Pokud je v některé z podmínek rovnováhy zastoupen kmitočet, je můstek kmitočtově závislý a lze ho použít nejen k měření impedancí, ale také k měření kmitočtů. Pro měření impedancí jsou výhodnější, kmitočtově nezávislé můstky. Střídavé můstky jsou napájeny z oscilátoru. Nulové indikátory (NI) indikují vyvážení můstku. K tomu se nejčastěji používá osciloskop. Abychom omezili vnější rušivé vlivy, musí být můstky pečlivě zeměny a stíněny.

Podmínka rovnováhy

<math>\mathbf{Z_1}\mathbf{Z_4}=\mathbf{Z_2}\mathbf{Z_3}</math>
<math>\mathbf{Z}=R\pm jX</math>

Dosadíme-li za jednotlivé hodnoty impedancí hodnoty v exponenciálním tvaru, bude platit:

<math>\mathbf{Z_1}e^{j\varphi_1}\mathbf{Z_4}e^{j\varphi_4}=\mathbf{Z_2}e^{j\varphi_2}\mathbf{Z_3}e^{j\varphi_3}</math>
<math>\mathbf{Z_1}\mathbf{Z_4}e^{j(\varphi_1+\varphi_4)}=\mathbf{Z_2}\mathbf{Z_3}e^{j(\varphi_2+\varphi_3)}</math>

Když tuto rovnici rozdělíme na dvě skalární, dostaneme dvě podmínky rovnováhy.

<math>|\mathbf{Z_1}||\mathbf{Z_4}|=|\mathbf{Z_2}||\mathbf{Z_3}|</math>
<math>\ \varphi_1+\varphi_4=\varphi_2+\varphi_3</math>

Číslicové měřiče impedancí

Číslicové měřiče impedancí mohou pracovat na různých principech, často se využívá převodník impedance-napětí nebo převodník admitance-napětí s využitím operačních zesilovačů.

Impedance a norma

S impedancí se lze také setkat při posuzování bezpečnosti elektrických instalací nn (například při revizích). Podmínky pro impedanci sítě TN (běžný druh sítě, nejčastěji používaný, např. i v bytových instalacích), stanoví ČSN 33 2000-4-41 ed.2 v článku 411.4.4. (dříve stará, dnes již neplatná ČSN 33 2000-4-41 v článku 413.1.3.3). Velikost impedance sítě TN určuje bezpečnost instalace tím, že je směrodatná pro rychlost vypnutí předřazeného jisticího přístroje (pojistka, jistič apod.). Aby jistící přístroj vypnul při poruše v dostatečně krátkém čase, musí být impedance dostatečně nízká. Podrobněji viz výše uvedená ČSN.

Odkazy

Související články

Externí odkazy

Literatura

  • SEDLÁK, Bedřich; ŠTOLL, Ivan. Elektřina a magnetismus. 2., opravené a rozšíření vyd. Praha : Academia, 2002. 632 s. ISBN 80-200-1004-1.  
  • Elektrotechnická měření. 1. vyd. Praha : nakladatelství BEN - technická literatura, 2002. 256 s. ISBN 80-7300-022-9.  
  • BLAHOVEC, Antonín. Elektrotechnika II. 4., nezměněné vyd. Praha : Informatorium, 2003. 156 s. ISBN 80-7333-013-X.  
  • DOLEČEK, Jaroslav. Moderní učebnice elektroniky. Praha : nakladatelství BEN - technická literatura, 2005. 344 s. ISBN 80-7300-146-2.  
Citováno z „http://ww.multimediaexpo.cz/mmecz/index.php/Impedance“