Multimediaexpo.cz je již 18 let na českém internetu !!
V tiskové zprávě k 18. narozeninám brzy najdete nové a zásadní informace.
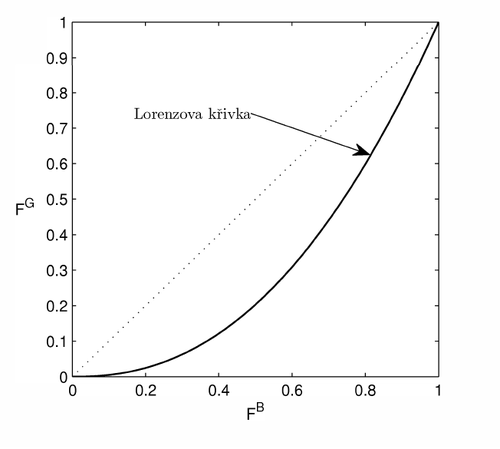
Lorenzova křivka
Z Multimediaexpo.cz
Lorenzova křivka je jedním z nejpoužívanějších způsobů grafického znázornění diverzifikace. V ekonomii se s ní často setkáváme především při znázorňování nerovnoměrnosti rozdělení důchodů či bohatství v populaci nějakého celku. Mezi další použití patří například hodnocení skóringových modelů.
Obsah |
Konstrukce Lorenzovy křivky
Ukažme konstrukci Lorenzovy křivky na příkladě měření diverzifikační schopnosti skóringového modelu. Konstrukce Lorenzovy křivky je založena na definici tzv. distribučních funkcí dobrých a špatných klientů.
Označme <math>S=\big\{s(\boldsymbol{x}), \boldsymbol{x}\in \boldsymbol{X}\big\}</math> obor hodnot skóringové funkce <math>s(\boldsymbol{x})</math>. Potom pro každou hodnotu skóre <math>s\in S</math> definujme distribuční funkci dobrých klientů <math>F^G(s)</math> jako pravděpodobnost, že náhodně vybraný dobrý klient (viz skóringový model) bude mít skóre menší než <math>s</math>, a distribuční funkci špatných klientů <math>F^B(s)</math> jako pravděpodobnost, že náhodně vybraný špatný klient bude mít skóre menší než <math>s</math>.
Explicitní distribuční funkce <math>F^G(s)</math> a <math>F^B(s)</math> v praxi zpravidla neznáme, proto je nejčastěji nahrazujeme konzistentními odhady. Funkci <math>F^G(s)</math> odhadujeme jako poměr počtu dobrých klientů se skóre menším než <math>s</math> ku počtu všech dobrých klientů a funkci <math>F^B(s)</math> jako poměr počtu špatných klientů se skóre menším než <math>s</math> ku počtu všech špatných klientů.
Nakonec definujeme Lorenzovu křivku jako množinu bodů
<math>L= \Big\{\big[F^B(s),F^G(s)\big]\in \mathbb{R}^2: s\in S \Big\}</math>,
kde <math>s\in S</math> nabývá všech hodnot použité skóringové funkce.
Takto zkonstruovaná Lorenzova křivka potom leží uvnitř jednotkového čtverce a spojuje protilehlé vrcholy, viz obrázek. Čím větší má náš model diverzifikační schopnost, tím více se Lorenzova křivka přibližuje stranám čtverce.
Obrázek Lorenzovy křivky
Příklad použití Lorenzovy křivky
Pokud osa "X" zobrazuje procento populace a osa "Y" procento bohatství ve společnosti (alternativně také důchodu), pak Lorenzova křivka (plná čára nahoře) uvádí, že 60% populace oné společnosti vlastní 30% z veškerého bohatství v této společnosti (alternativně, že na ní připadá 30% důchodu). Tečkovaná čára grafu by zobrazovala rovnostářskou společnost, kdy všichni jedinci dosahují identické úrovně svého bohatství (alternativně stejnou úroveň důchodu).
Související články
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |