Multimediaexpo.cz je již 18 let na českém internetu !!
V tiskové zprávě k 18. narozeninám brzy najdete nové a zásadní informace.
Úhlová velikost
Z Multimediaexpo.cz
Úhlová velikost objektu je úhel měřený pozorovatelem mezi krajními body objektu.
Obvyklé použití je v astronomii, kde se používá i termín úhlový průměr nebo zdánlivý průměr pro úhlovou velikost hvězdných těles (jde o úhlovou velikost tělesům a jevům průměru opsaného kruhu).
S úhlovou velikostí souvisí i astronomická jednotka parsek (značka pc): Jeden parsek je vzdálenost, z které je úhlová velikost poloměru oběžné dráhy Země (cca 150 milionu km) rovna 1" (jedné úhlové vteřině).
Respektive objekt ve vzdálenosti 1 pc se bude jevit na astronomických snímcích pořízených s odstupem půl roku až o 2 úhlové vteřiny posunutý.
Definice
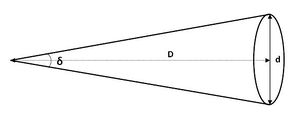
Matematicky je úhlová velikost \(\delta\) dána rovnicí:
- \(\delta = 2 \arctan \left( \frac{1}{2}\,d / D \right),\)
kde \(\delta\) je úhlový průměr, \(d\) je zdánlivý (viděný) průměr tělesa a \(D\) je vzdálenost k objektu, vyjádřené ve shodných jednotkách. Pokud je \(D\) mnohem větší než \(d\), můžeme aproximovat \(\delta\) pomocí rovnosti \(\delta = d / D\), odkud získáme výsledek v radiánech.
Úhlová velikost je potom přímo úměrná velikosti objektu a nepřímo úměrná jeho vzdálenosti od pozorovatele.
Pro sférický (kulový) objekt, jehož vlastní průměr je roven \(d_\mbox{act}\), můžeme hledat úhlový průměr \(\delta\) pomocí vztahu:
- \(\delta = 2 \arcsin \left( \frac{1}{2}\,d_\mbox{act} / D \right);\)
v praktických aplikacích je rozdíl mezi \(d\) a \(d_\mbox{act}\) významný pouze u sférických objektů, které jsou relativně blízko.
Související články
Externí odkazy
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |