V pondělí 16. září 2024 začala naše další
nová soutěž o nejlepší webovou stránku !!
Proto neváhejte a začněte rychle soutěžit o lákavé ceny !!

Limita

Z Multimediaexpo.cz

(Rozdíly mezi verzemi)
m (1 revizi)
m (Nahrazení textu „<math>“ textem „<big>\(“)
Řádka 1: Řádka 1:
:''Tento článek pojednává o limitě funkce nebo zobrazení. O limitě a kolimitě v teorii kategorií je článek [[Limita (teorie kategorií)]]''
:''Tento článek pojednává o limitě funkce nebo zobrazení. O limitě a kolimitě v teorii kategorií je článek [[Limita (teorie kategorií)]]''
-
'''Limita''' je [[matematika|matematická]] konstrukce, vyjadřující, že se hodnoty zadané [[posloupnost]]i nebo [[funkce (matematika)|funkce]] blíží libovolně blízko k nějakému bodu. Právě tento bod je pak označován jako limita. Tato skutečnost se u funkcí zapisuje <math>\lim_{z\rightarrow z_0} f(z)=a</math> a u posloupností <math>\lim_{n\to\infty} a_n=a</math> případně <math>a _n \to a\,</math>.
+
'''Limita''' je [[matematika|matematická]] konstrukce, vyjadřující, že se hodnoty zadané [[posloupnost]]i nebo [[funkce (matematika)|funkce]] blíží libovolně blízko k nějakému bodu. Právě tento bod je pak označován jako limita. Tato skutečnost se u funkcí zapisuje <big>\(\lim_{z\rightarrow z_0} f(z)=a</math> a u posloupností <big>\(\lim_{n\to\infty} a_n=a</math> případně <big>\(a _n \to a\,</math>.
Dle toho, zda se uvažuje o posloupnosti nebo o funkci, hovoříme o [[limita posloupnosti|limitě posloupnosti]] nebo [[limita funkce|limitě funkce]]. Pojem limity lze definovat na libovolném [[metrický prostor|metrickém prostoru]].
Dle toho, zda se uvažuje o posloupnosti nebo o funkci, hovoříme o [[limita posloupnosti|limitě posloupnosti]] nebo [[limita funkce|limitě funkce]]. Pojem limity lze definovat na libovolném [[metrický prostor|metrickém prostoru]].
== Limita posloupnosti ==
== Limita posloupnosti ==
{{Hlavní článek|Limita posloupnosti}}
{{Hlavní článek|Limita posloupnosti}}
-
[[Posloupnost (matematika)|Posloupnost]] <math>\left( a_n \right) _{n=1} ^\infty</math> má ''limitu A'', pokud se jejími hodnotami můžeme k A libovolně přiblížit. Tedy pro každé kladné číslo <math>\varepsilon</math> platí, že existuje nějaký člen posloupnosti, od kterého jsou už její hodnoty od ''A'' vzdáleny méně, než <math>\varepsilon</math>.
+
[[Posloupnost (matematika)|Posloupnost]] <big>\(\left( a_n \right) _{n=1} ^\infty</math> má ''limitu A'', pokud se jejími hodnotami můžeme k A libovolně přiblížit. Tedy pro každé kladné číslo <big>\(\varepsilon</math> platí, že existuje nějaký člen posloupnosti, od kterého jsou už její hodnoty od ''A'' vzdáleny méně, než <big>\(\varepsilon</math>.
Zapsáno symbolicky:
Zapsáno symbolicky:
-
:<math>\forall \varepsilon > 0: \exists n \in \mathbb{N} : \forall k \geq n : \left| a _k - A \right| < \varepsilon</math>
+
:<big>\(\forall \varepsilon > 0: \exists n \in \mathbb{N} : \forall k \geq n : \left| a _k - A \right| < \varepsilon</math>
== Limita funkce ==
== Limita funkce ==
{{Hlavní článek|limita funkce}}
{{Hlavní článek|limita funkce}}
-
Říkáme, že [[Funkce (matematika)|funkce]] ''f(x)'' má v bodě ''a limitu A'', jestliže k libovolnému <math>\epsilon >0</math> existuje takové <math>\delta > 0</math> , že pro všechna ''x'' z <math>\delta</math>-[[okolí (matematika)|okolí]] bodu ''a'', z něhož vyjmeme bod ''a'' (tzv. prstencová okolí bodu ''a'') je <math>\left| f(x)-A \right|< \epsilon, </math>.
+
Říkáme, že [[Funkce (matematika)|funkce]] ''f(x)'' má v bodě ''a limitu A'', jestliže k libovolnému <big>\(\epsilon >0</math> existuje takové <big>\(\delta > 0</math> , že pro všechna ''x'' z <big>\(\delta</math>-[[okolí (matematika)|okolí]] bodu ''a'', z něhož vyjmeme bod ''a'' (tzv. prstencová okolí bodu ''a'') je <big>\(\left| f(x)-A \right|< \epsilon, </math>.
== Limita vzhledem k podmnožině ==
== Limita vzhledem k podmnožině ==
(Speciální případ: Pravostranná a levostranná limita)
(Speciální případ: Pravostranná a levostranná limita)
== Vlastní a nevlastní limita ==
== Vlastní a nevlastní limita ==
-
Limitou posloupnosti [[Rozšířená_reálná_čísla#Limita_posloupnosti|může být]] nejen číslo (tj. vlastní limita), ale i symbol <math>+\infty \,\!</math> nebo <math>-\infty \,\!</math> (nevlastní limita).  
+
Limitou posloupnosti [[Rozšířená_reálná_čísla#Limita_posloupnosti|může být]] nejen číslo (tj. vlastní limita), ale i symbol <big>\(+\infty \,\!</math> nebo <big>\(-\infty \,\!</math> (nevlastní limita).  
-
Limitu funkce [[Rozšířená_reálná_čísla#Limita_funkce|lze zkoumat]] ve vlastním bodě (v reálném čísle), tak i v [[Nevlastní bod|nevlastním bodě]] <math>+\infty \,\!</math> nebo <math>-\infty \,\!</math>. V obou případech může být limita vlastní, nevlastní nebo limita nemusí existovat.
+
Limitu funkce [[Rozšířená_reálná_čísla#Limita_funkce|lze zkoumat]] ve vlastním bodě (v reálném čísle), tak i v [[Nevlastní bod|nevlastním bodě]] <big>\(+\infty \,\!</math> nebo <big>\(-\infty \,\!</math>. V obou případech může být limita vlastní, nevlastní nebo limita nemusí existovat.
== Zobecnění pro topologické prostory ==
== Zobecnění pro topologické prostory ==
-
Limita zobrazení <math>f: A\to B</math> mezi [[topologický prostor|topologickými prostory]] je v bodě ''a'' definována jako <math>b\in B</math> takové, že pro každé okolí ''O(b)'' bodu ''b'' existuje okolí ''O(a)'' bodu ''a'' takové, že <math>x\in O(a)</math> implikuje <math>f(x)\in O(b)</math>.  
+
Limita zobrazení <big>\(f: A\to B</math> mezi [[topologický prostor|topologickými prostory]] je v bodě ''a'' definována jako <big>\(b\in B</math> takové, že pro každé okolí ''O(b)'' bodu ''b'' existuje okolí ''O(a)'' bodu ''a'' takové, že <big>\(x\in O(a)</math> implikuje <big>\(f(x)\in O(b)</math>.  
Dalším zobecněním limity posloupnosti, funkce i zobrazení jsou limity [[Síť (topologie)|sítí]]<ref>Michael C. Gemignani, Elementary topology, Courier Dover Publications, 1990 (strana 122, def. 3)</ref>.  
Dalším zobecněním limity posloupnosti, funkce i zobrazení jsou limity [[Síť (topologie)|sítí]]<ref>Michael C. Gemignani, Elementary topology, Courier Dover Publications, 1990 (strana 122, def. 3)</ref>.  
Limita zobrazení nebo sítě může být v obecném topologickém prostoru víceznačná. Platí však, že v [[Hausdorffův prostor|Hausdorffově prostoru]], je tato limita jednoznačná, t.j. každá síť má nejvýše jednu limitu.
Limita zobrazení nebo sítě může být v obecném topologickém prostoru víceznačná. Platí však, že v [[Hausdorffův prostor|Hausdorffově prostoru]], je tato limita jednoznačná, t.j. každá síť má nejvýše jednu limitu.
=== Příklady ===
=== Příklady ===
<gallery widths="240" heights="180">
<gallery widths="240" heights="180">
-
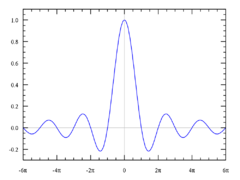
Soubor:Sinc function (unnormalized).png|Graf funkce <math>\scriptstyle f(x) = \frac{\sin(x)}{x}</math>. Je vidět, že tato funkce má limitu 1 v bodě nula.
+
Soubor:Sinc function (unnormalized).png|Graf funkce <big>\(\scriptstyle f(x) = \frac{\sin(x)}{x}</math>. Je vidět, že tato funkce má limitu 1 v bodě nula.
-
Soubor:Graph of function 1 to minus 1 in Neighbourhood of zero.png|Graf funkce <math>\scriptstyle f(x) = \frac{1}{x} </math>. Je vidět, že tato funkce nemá limitu v bodě nula a má vlastní limity 0 v <math>\scriptstyle \pm \infty</math>.  
+
Soubor:Graph of function 1 to minus 1 in Neighbourhood of zero.png|Graf funkce <big>\(\scriptstyle f(x) = \frac{1}{x} </math>. Je vidět, že tato funkce nemá limitu v bodě nula a má vlastní limity 0 v <big>\(\scriptstyle \pm \infty</math>.  
-
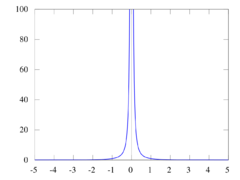
Soubor:1 to minus 2.png|Graf funkce <math>\scriptstyle f(x) = \frac{1}{x^2}</math>. Je vidět, že tato funkce má nevlastní limitu <math>\scriptstyle  +\infty \,\!</math> v bodě nula a má vlastní limity 0 v <math>\scriptstyle \pm \infty</math>.  
+
Soubor:1 to minus 2.png|Graf funkce <big>\(\scriptstyle f(x) = \frac{1}{x^2}</math>. Je vidět, že tato funkce má nevlastní limitu <big>\(\scriptstyle  +\infty \,\!</math> v bodě nula a má vlastní limity 0 v <big>\(\scriptstyle \pm \infty</math>.  
</gallery>
</gallery>
-
* Funkce <math>{\sin x}\over x \,\!</math> není v nule definovaná, ale má v ní limitu 1<ref group=pozn>To lze intuitivně zdůvodnit tak, že funkce ''sin x'' má v okolí nuly "velmi podobný" průběh, jako funkce f(x) = x; proto se jejich poměr blíží k jedné.</ref> (vlastní limita ve vlastním bodě) a v <math>+\infty \,\!</math> má limitu 0 (vlastní limita v nevlastním bodě).
+
* Funkce <big>\({\sin x}\over x \,\!</math> není v nule definovaná, ale má v ní limitu 1<ref group=pozn>To lze intuitivně zdůvodnit tak, že funkce ''sin x'' má v okolí nuly "velmi podobný" průběh, jako funkce f(x) = x; proto se jejich poměr blíží k jedné.</ref> (vlastní limita ve vlastním bodě) a v <big>\(+\infty \,\!</math> má limitu 0 (vlastní limita v nevlastním bodě).
-
* Funkce <math>{\sin x} \,\!</math> je v nule [[Spojitá funkce|spojitá]] (limita je 0) a v <math>+\infty \,\!</math> limitu nemá. Obě tato tvrzení platí i o funkci <math>{x \cdot \sin x} \,\!</math>
+
* Funkce <big>\({\sin x} \,\!</math> je v nule [[Spojitá funkce|spojitá]] (limita je 0) a v <big>\(+\infty \,\!</math> limitu nemá. Obě tato tvrzení platí i o funkci <big>\({x \cdot \sin x} \,\!</math>
-
* Funkce <math>{\sin {1\over x}} \,\!</math> ani <math>{\sin {1\over x}}\over x \,\!</math> v nule limitu nemají. Totéž platí i o funkcích <math>{1\over x}\,\!</math> či <math>{1\over x^3}\,\!</math>, ovšem ty mají alespoň jednostranné limity: jejich pravostranná limita je <math>+\infty \,\!</math> a levostranná <math>-\infty \,\!</math>. Naproti tomu funkce <math>{1\over x^2}\,\!</math> a <math>{1\over x^4}\,\!</math> mají v nule limitu <math>+\infty \,\!</math> (nevlastní limita ve vlastním bodě).
+
* Funkce <big>\({\sin {1\over x}} \,\!</math> ani <big>\({\sin {1\over x}}\over x \,\!</math> v nule limitu nemají. Totéž platí i o funkcích <big>\({1\over x}\,\!</math> či <big>\({1\over x^3}\,\!</math>, ovšem ty mají alespoň jednostranné limity: jejich pravostranná limita je <big>\(+\infty \,\!</math> a levostranná <big>\(-\infty \,\!</math>. Naproti tomu funkce <big>\({1\over x^2}\,\!</math> a <big>\({1\over x^4}\,\!</math> mají v nule limitu <big>\(+\infty \,\!</math> (nevlastní limita ve vlastním bodě).
-
* Funkce <math>e^x\,\!</math> má v <math>-\infty \,\!</math> limitu 0 (vlastní limita v nevlastním bodě) a v <math>+\infty \,\!</math> limitu <math>+\infty \,\!</math>.
+
* Funkce <big>\(e^x\,\!</math> má v <big>\(-\infty \,\!</math> limitu 0 (vlastní limita v nevlastním bodě) a v <big>\(+\infty \,\!</math> limitu <big>\(+\infty \,\!</math>.
== Poznámky ==
== Poznámky ==
<references group="pozn"/>
<references group="pozn"/>

Verze z 14. 8. 2022, 14:49

Tento článek pojednává o limitě funkce nebo zobrazení. O limitě a kolimitě v teorii kategorií je článek Limita (teorie kategorií)

Limita je matematická konstrukce, vyjadřující, že se hodnoty zadané posloupnosti nebo funkce blíží libovolně blízko k nějakému bodu. Právě tento bod je pak označován jako limita. Tato skutečnost se u funkcí zapisuje \(\lim_{z\rightarrow z_0} f(z)=a</math> a u posloupností \(\lim_{n\to\infty} a_n=a</math> případně \(a _n \to a\,</math>. Dle toho, zda se uvažuje o posloupnosti nebo o funkci, hovoříme o limitě posloupnosti nebo limitě funkce. Pojem limity lze definovat na libovolném metrickém prostoru.

Obsah

Limita posloupnosti

Hlavní článek: Limita posloupnosti

Posloupnost \(\left( a_n \right) _{n=1} ^\infty</math> má limitu A, pokud se jejími hodnotami můžeme k A libovolně přiblížit. Tedy pro každé kladné číslo \(\varepsilon</math> platí, že existuje nějaký člen posloupnosti, od kterého jsou už její hodnoty od A vzdáleny méně, než \(\varepsilon</math>. Zapsáno symbolicky:

\(\forall \varepsilon > 0: \exists n \in \mathbb{N} : \forall k \geq n : \left| a _k - A \right| < \varepsilon</math>

Limita funkce

Hlavní článek: limita funkce

Říkáme, že funkce f(x) má v bodě a limitu A, jestliže k libovolnému \(\epsilon >0</math> existuje takové \(\delta > 0</math> , že pro všechna x z \(\delta</math>-okolí bodu a, z něhož vyjmeme bod a (tzv. prstencová okolí bodu a) je \(\left| f(x)-A \right|< \epsilon, </math>.

Limita vzhledem k podmnožině

(Speciální případ: Pravostranná a levostranná limita)

Vlastní a nevlastní limita

Limitou posloupnosti může být nejen číslo (tj. vlastní limita), ale i symbol \(+\infty \,\!</math> nebo \(-\infty \,\!</math> (nevlastní limita). Limitu funkce lze zkoumat ve vlastním bodě (v reálném čísle), tak i v nevlastním bodě \(+\infty \,\!</math> nebo \(-\infty \,\!</math>. V obou případech může být limita vlastní, nevlastní nebo limita nemusí existovat.

Zobecnění pro topologické prostory

Limita zobrazení \(f: A\to B</math> mezi topologickými prostory je v bodě a definována jako \(b\in B</math> takové, že pro každé okolí O(b) bodu b existuje okolí O(a) bodu a takové, že \(x\in O(a)</math> implikuje \(f(x)\in O(b)</math>. Dalším zobecněním limity posloupnosti, funkce i zobrazení jsou limity sítí[1]. Limita zobrazení nebo sítě může být v obecném topologickém prostoru víceznačná. Platí však, že v Hausdorffově prostoru, je tato limita jednoznačná, t.j. každá síť má nejvýše jednu limitu.

Příklady

Graf funkce \(\scriptstyle f(x) = \frac{\sin(x)}{x}</math>. Je vidět, že tato funkce má limitu 1 v bodě nula.

Graf funkce \(\scriptstyle f(x) = \frac{1}{x} </math>. Je vidět, že tato funkce nemá limitu v bodě nula a má vlastní limity 0 v \(\scriptstyle \pm \infty</math>.

Graf funkce \(\scriptstyle f(x) = \frac{1}{x^2}</math>. Je vidět, že tato funkce má nevlastní limitu \(\scriptstyle +\infty \,\!</math> v bodě nula a má vlastní limity 0 v \(\scriptstyle \pm \infty</math>.

  • Funkce \({\sin x}\over x \,\!</math> není v nule definovaná, ale má v ní limitu 1[pozn 1] (vlastní limita ve vlastním bodě) a v \(+\infty \,\!</math> má limitu 0 (vlastní limita v nevlastním bodě).
  • Funkce \({\sin x} \,\!</math> je v nule spojitá (limita je 0) a v \(+\infty \,\!</math> limitu nemá. Obě tato tvrzení platí i o funkci \({x \cdot \sin x} \,\!</math>
  • Funkce \({\sin {1\over x}} \,\!</math> ani \({\sin {1\over x}}\over x \,\!</math> v nule limitu nemají. Totéž platí i o funkcích \({1\over x}\,\!</math> či \({1\over x^3}\,\!</math>, ovšem ty mají alespoň jednostranné limity: jejich pravostranná limita je \(+\infty \,\!</math> a levostranná \(-\infty \,\!</math>. Naproti tomu funkce \({1\over x^2}\,\!</math> a \({1\over x^4}\,\!</math> mají v nule limitu \(+\infty \,\!</math> (nevlastní limita ve vlastním bodě).
  • Funkce \(e^x\,\!</math> má v \(-\infty \,\!</math> limitu 0 (vlastní limita v nevlastním bodě) a v \(+\infty \,\!</math> limitu \(+\infty \,\!</math>.

Poznámky

  1. ↑ To lze intuitivně zdůvodnit tak, že funkce sin x má v okolí nuly "velmi podobný" průběh, jako funkce f(x) = x; proto se jejich poměr blíží k jedné.

Související články

Reference

  1. ↑ Michael C. Gemignani, Elementary topology, Courier Dover Publications, 1990 (strana 122, def. 3)


Citováno z „http://ww.multimediaexpo.cz/mmecz/index.php/Limita“