Multimediaexpo.cz je již 18 let na českém internetu !!
V tiskové zprávě k 18. narozeninám brzy najdete nové a zásadní informace.
Eulerova konstanta
Z Multimediaexpo.cz
m (Nahrazení textu „<math>“ textem „<big>\(“) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| Řádka 8: | Řádka 8: | ||
Nejsnadneji lze tuto konstantu definovat jako následující limitu: | Nejsnadneji lze tuto konstantu definovat jako následující limitu: | ||
| - | <big>\(\gamma = \lim_{n \to \infty} \left(1+\frac{1}{2}+\frac{1}{3}+\dots + \frac{1}{n}-\ln n \right)</ | + | <big>\(\gamma = \lim_{n \to \infty} \left(1+\frac{1}{2}+\frac{1}{3}+\dots + \frac{1}{n}-\ln n \right)\)</big> |
| - | Je obecně známo, že harmonická řada vyskytující se v limitě je řadou divergentní, má tedy nekonečný součet. To že výše uvedená limita je vlastní označuje skutečnost, že pro velká <big>\(n</ | + | Je obecně známo, že harmonická řada vyskytující se v limitě je řadou divergentní, má tedy nekonečný součet. To že výše uvedená limita je vlastní označuje skutečnost, že pro velká <big>\(n\)</big> můžeme součet harmonické řady aproximovat přirozeným logaritmem, jenž je v nekonečnu taktéž nekonečný. |
== Geometrická představa == | == Geometrická představa == | ||
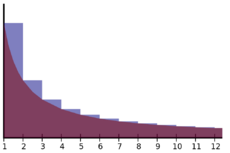
[[Soubor:Gamma-area.png|thumb|230px|Obsah modré plochy se rovná Eulerově konstantě]] | [[Soubor:Gamma-area.png|thumb|230px|Obsah modré plochy se rovná Eulerově konstantě]] | ||
| - | Hodnotu konstanty <big>\(\gamma</ | + | Hodnotu konstanty <big>\(\gamma\)</big> si můžeme představit i geometricky. Zobrazíme-li grafy funkci |
| - | <big>\(f(x)=\frac{1}{\lfloor x \rfloor},</ | + | <big>\(f(x)=\frac{1}{\lfloor x \rfloor},\)</big> |
| - | <big>\(g(x)=\frac{1}{x},</ | + | <big>\(g(x)=\frac{1}{x},\)</big> |
| - | kde <big>\(\lfloor x \rfloor</ | + | kde <big>\(\lfloor x \rfloor\)</big> značí (dolní) [[celá část|celou část]] čísla <big>\(x\)</big>, pak obsah plochy mezi těmito dvěma grafy pro x od 1 do nekonečna je právě roven Eulerově konstantě <big>\(\gamma\)</big>: |
| - | <big>\(\gamma= \int_1^\infty \left( \frac{1}{\lfloor x \rfloor} - \frac{1}{x}\right) dx.</ | + | <big>\(\gamma= \int_1^\infty \left( \frac{1}{\lfloor x \rfloor} - \frac{1}{x}\right) dx.\)</big> |
== Reference == | == Reference == | ||
Aktuální verze z 14. 8. 2022, 14:51
| Tento článek potřebuje úpravy. Můžete Multimediaexpo.cz pomoci tím, že ho vylepšíte. Jak by měly články vypadat, popisují stránky Vzhled a styl a Encyklopedický styl. |
|
- Možná hledáte: Eulerovo číslo
Eulerova konstanta nebo též Eulerova–Mascheroniho konstanta je matematická konstanta používaná v teorii čísel a v analýze. O této konstantě není známo, zda je racionální či iracionální.[1]
Eulerova konstanta je přibližně rovna: 0,57721 56649 01532 86060 65120 90082 40243 10421 59335 93992 … .[2]
Obsah |
Definice
Nejsnadneji lze tuto konstantu definovat jako následující limitu:
\(\gamma = \lim_{n \to \infty} \left(1+\frac{1}{2}+\frac{1}{3}+\dots + \frac{1}{n}-\ln n \right)\)
Je obecně známo, že harmonická řada vyskytující se v limitě je řadou divergentní, má tedy nekonečný součet. To že výše uvedená limita je vlastní označuje skutečnost, že pro velká \(n\) můžeme součet harmonické řady aproximovat přirozeným logaritmem, jenž je v nekonečnu taktéž nekonečný.
Geometrická představa
Hodnotu konstanty \(\gamma\) si můžeme představit i geometricky. Zobrazíme-li grafy funkci
\(f(x)=\frac{1}{\lfloor x \rfloor},\)
\(g(x)=\frac{1}{x},\)
kde \(\lfloor x \rfloor\) značí (dolní) celou část čísla \(x\), pak obsah plochy mezi těmito dvěma grafy pro x od 1 do nekonečna je právě roven Eulerově konstantě \(\gamma\):
\(\gamma= \int_1^\infty \left( \frac{1}{\lfloor x \rfloor} - \frac{1}{x}\right) dx.\)
Reference
Externí odkazy
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |