Funkce (matematika)
Z Multimediaexpo.cz
(+ Masivní vylepšení) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| (Není zobrazena jedna mezilehlá verze.) | |||
| Řádka 5: | Řádka 5: | ||
Na [[množina|množině]] [[číslo|čísel]] M je definovaná '''funkce''', je-li dán předpis, podle kterého je každému ''x'' náležícímu do množiny ''M'' přiřazeno právě jedno číslo ''y''. | Na [[množina|množině]] [[číslo|čísel]] M je definovaná '''funkce''', je-li dán předpis, podle kterého je každému ''x'' náležícímu do množiny ''M'' přiřazeno právě jedno číslo ''y''. | ||
| - | Značíme: '''< | + | Značíme: '''<big>\(y=f(x)\)</big>'''. |
| - | [[Proměnná]] < | + | [[Proměnná]] <big>\(x\)</big> se označuje jako '''argument funkce''' ('''nezávisle proměnná'''). Proměnná <big>\(y\)</big> je '''funkční hodnota''' ('''závisle proměnná'''). |
M nazýváme [[definiční obor|definičním oborem]] funkce. Pokud není při zadání funkce uveden definiční obor, pak se za definiční obor obvykle považuje množina všech hodnot nezávisle proměnné, pro něž má funkce smysl. Definičním oborem může být například množina [[celé číslo|celých]], [[reálné číslo|reálných]] nebo [[komplexní číslo|komplexních čísel]]. Definiční obor může mít i více [[Dimenze vektorového prostoru|dimenzí]]. Pokud má dvě, pak můžeme říkat, že má [[funkce]] dva [[argument]]y, nebo že jejím argumentem je jeden dvourozměrný [[vektor]]. Jedná se o dva pohledy na stejnou věc. V případě, že má [[vektor]], který je argumentem funkce, nekonečnou [[Dimenze vektorového prostoru|dimenzi]] (většinou [[nespočetná množina|nespočetnou]]), nemluvíme již o [[funkce|funkci]], ale o [[funkcionál]]u. | M nazýváme [[definiční obor|definičním oborem]] funkce. Pokud není při zadání funkce uveden definiční obor, pak se za definiční obor obvykle považuje množina všech hodnot nezávisle proměnné, pro něž má funkce smysl. Definičním oborem může být například množina [[celé číslo|celých]], [[reálné číslo|reálných]] nebo [[komplexní číslo|komplexních čísel]]. Definiční obor může mít i více [[Dimenze vektorového prostoru|dimenzí]]. Pokud má dvě, pak můžeme říkat, že má [[funkce]] dva [[argument]]y, nebo že jejím argumentem je jeden dvourozměrný [[vektor]]. Jedná se o dva pohledy na stejnou věc. V případě, že má [[vektor]], který je argumentem funkce, nekonečnou [[Dimenze vektorového prostoru|dimenzi]] (většinou [[nespočetná množina|nespočetnou]]), nemluvíme již o [[funkce|funkci]], ale o [[funkcionál]]u. | ||
| - | Množinu všech čísel < | + | Množinu všech čísel <big>\(\ f(x)\)</big>, takových, že <big>\(x \in\ M\)</big>, nazýváme [[obor hodnot|oborem hodnot]] dané funkce. |
=== Matematicky přesnější === | === Matematicky přesnější === | ||
| - | '''Funkce''' < | + | '''Funkce''' <big>\(f\)</big> je podmnožina součinu <big>\(M\times T\)</big>, kde M a T jsou množiny, T je obvykle podmnožina reálných nebo komplexních čísel, taková, že pro každý prvek ''m'' [[množina|množiny]] ''M'' existuje nejvýše jedna uspořádaná dvojice <big>\([m,x]\in f\)</big>. Obvykle píšeme <big>\(f(m)=x\)</big>. |
'''Definičním oborem''' funkce je pak podmnožina všech prvků množiny ''M'', ke kterým taková uspořádaná dvojice existuje právě jedna. Říkáme, že pro prvky množiny ''M'', které nejsou prvky definičního oboru, daná funkce '''není definována'''. | '''Definičním oborem''' funkce je pak podmnožina všech prvků množiny ''M'', ke kterým taková uspořádaná dvojice existuje právě jedna. Říkáme, že pro prvky množiny ''M'', které nejsou prvky definičního oboru, daná funkce '''není definována'''. | ||
| - | '''Oborem hodnot''' dané funkce je množina všech prvků ''x'' množiny ''T'', ke kterým v relaci existuje alespoň jedna uspořádaná dvojice < | + | '''Oborem hodnot''' dané funkce je množina všech prvků ''x'' množiny ''T'', ke kterým v relaci existuje alespoň jedna uspořádaná dvojice <big>\([m,x]\in f\)</big>, kde <big>\(m \in M\)</big>. |
== Způsoby zadání funkce == | == Způsoby zadání funkce == | ||
=== Analyticky === | === Analyticky === | ||
| - | Analytickým předpisem rozumíme zadání funkce ve formě < | + | Analytickým předpisem rozumíme zadání funkce ve formě <big>\(y = f(x)\)</big>, pak říkáme, že funkce je zadána ''explicitním vyjádřením'' ('''explicitní funkce'''). Funkci můžeme vyjádřit také v ''implicitním tvaru'' ('''implicitní funkce''') jako <big>\(F(x,y) = 0\)</big>. Dalším způsobem je zápis v ''parametrickém tvaru'' ('''parametrická funkce''') [[soustava rovnic|soustavou rovnic]] <big>\(x = f_1(t)\)</big>, <big>\(y = f_2(t)\)</big>, kde <big>\(t\)</big> je vhodný parametr. |
==== Příklad ==== | ==== Příklad ==== | ||
| - | Např. < | + | Např. <big>\(y = 2x^2\)</big> je explicitní zápis [[kvadratická funkce|kvadratické funkce]]. V implicitním tvaru lze stejnou rovnici zapsat jako <big>\(y - 2x^2 = 0\)</big>. V parametrickém tvaru lze zvolit např. soustavu rovnic <big>\(x = \frac{t}{\sqrt{2}}\)</big>, <big>\(y = t^2\)</big>. |
=== Graficky === | === Graficky === | ||
Při grafickém zadání funkci vyjádříme [[graf (funkce)|grafem]]. | Při grafickém zadání funkci vyjádříme [[graf (funkce)|grafem]]. | ||
==== Příklad ==== | ==== Příklad ==== | ||
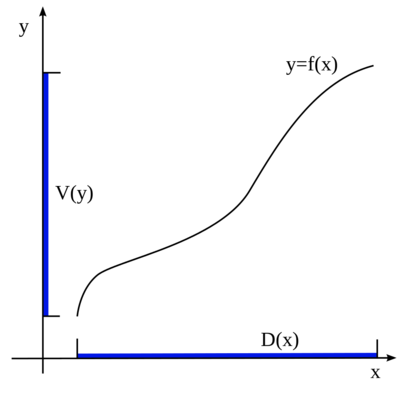
| - | Příklad zadání funkce grafem (< | + | Příklad zadání funkce grafem (<big>\(D(x)\)</big> označuje definiční obor a <big>\(V(y)\)</big> obor hodnot) |
[[Soubor:Zadani funkce grafem.png|center|400px|Zadání funkce grafem.]] | [[Soubor:Zadani funkce grafem.png|center|400px|Zadání funkce grafem.]] | ||
| Řádka 37: | Řádka 37: | ||
Příkladem může být např. zadání funkce | Příkladem může být např. zadání funkce | ||
{| class="wikitable" | {| class="wikitable" | ||
| - | | < | + | | <big>\(x\)</big> || 1 || 2 || 3 || 7 || 9 |
|- | |- | ||
| - | | < | + | | <big>\(y\)</big> || 2 || 4 || 5 || 3 || 3 |
|} | |} | ||
| - | Definičním oborem je zde množina < | + | Definičním oborem je zde množina <big>\(\{1,2,3,7,9\}\)</big> a oborem hodnot je množina <big>\(\{2,3,4,5\} \)</big>. |
== Typy funkcí == | == Typy funkcí == | ||
| Řádka 49: | Řádka 49: | ||
Argumentem funkce nemusí být jen [[číslo|čísla]], ale mohou jím být také [[matice]], [[vektor]]y, [[tenzor]]y, apod. Pak podle typu argumentu hovoříme o [[maticová funkce|maticové funkci]], [[vektorová funkce|vektorové funkci]], [[tenzorová funkce|tenzorové funkci]], apod. | Argumentem funkce nemusí být jen [[číslo|čísla]], ale mohou jím být také [[matice]], [[vektor]]y, [[tenzor]]y, apod. Pak podle typu argumentu hovoříme o [[maticová funkce|maticové funkci]], [[vektorová funkce|vektorové funkci]], [[tenzorová funkce|tenzorové funkci]], apod. | ||
| - | O funkci obsahující jedinou nezávisle proměnnou hovoříme jako o ''funkci jedné proměnné'', např. < | + | O funkci obsahující jedinou nezávisle proměnnou hovoříme jako o ''funkci jedné proměnné'', např. <big>\(y = f(x)\)</big>. Funkce obsahující dvě (nebo více) nezávislých proměnných pak označujeme jako ''funkci dvou (tří, čtyř, …) proměnných'', např. <big>\(z = f(x,y)\)</big> je funkce dvou proměnných <big>\(x\)</big> a <big>\(y\)</big>. Funkci <big>\(n\)</big>-proměnných zapisujeme jako |
| - | * < | + | * <big>\(f(x_1,x_2,..., x_n)\)</big> |
| - | * < | + | * <big>\(f(x_i)\)</big> pro <big>\(i=1,2,...,n\)</big> |
| - | * < | + | * <big>\(f(X)\)</big>, kde <big>\(X = [x_1,x_2,...,x_n]\)</big> představuje [[bod]] v n-rozměrném [[vektorový prostor|prostoru]] |
| - | * < | + | * <big>\(f(r)\)</big>, kde <big>\(r\)</big> představuje [[polohový vektor]] bodu v n-rozměrném prostoru. |
=== Algebraická a transcendentní funkce === | === Algebraická a transcendentní funkce === | ||
| - | Funkci označujeme jako ''algebraickou'', pokud ji lze vyjádřit ve tvaru [[polynom]]u, např. pokud lze funkci < | + | Funkci označujeme jako ''algebraickou'', pokud ji lze vyjádřit ve tvaru [[polynom]]u, např. pokud lze funkci <big>\(y = f(x)\)</big> vyjádřit jako <big>\(P(x,y) = 0\)</big>, kde <big>\(P\)</big> je polynom, pak se jedná o algebraickou funkci. [[Polynom#Stupeň polynomu|Stupeň polynomu]] <big>\(P\)</big> pak určuje stupeň funkce. Funkce, které nejsou algebraické, označujeme jako ''transcendentní''. Mezi transcendentní funkce se řadí funkce sin, cos, tg, cotg, exp, log, případně další, které nejdou vyjádřit pomocí elementárních funkcí. |
| - | Algebraické funkce lze dále rozdělit na ''[[racionální funkce]]'' a ''[[iracionální funkce]]''. Iracionální funkce jsou funkce obsahující < | + | Algebraické funkce lze dále rozdělit na ''[[racionální funkce]]'' a ''[[iracionální funkce]]''. Iracionální funkce jsou funkce obsahující <big>\(x^{\frac{m}{n}}\)</big>, kde <big>\(m, n\)</big> jsou [[nesoudělná čísla]]. |
Transcendentní funkce lze rozdělit na ''nižší'', kam patří např. [[exponenciální funkce|exponenciální]], [[logaritmická funkce|logaritmické]], [[goniometrická funkce|goniometrické]] a [[cyklometrické funkce]], a ''vyšší''. Vyšší transcendentní funkce nelze pomocí [[elementární funkce|elementárních funkcí]] vyjádřit v konečném tvaru. | Transcendentní funkce lze rozdělit na ''nižší'', kam patří např. [[exponenciální funkce|exponenciální]], [[logaritmická funkce|logaritmické]], [[goniometrická funkce|goniometrické]] a [[cyklometrické funkce]], a ''vyšší''. Vyšší transcendentní funkce nelze pomocí [[elementární funkce|elementárních funkcí]] vyjádřit v konečném tvaru. | ||
| Řádka 65: | Řádka 65: | ||
Zvláštním případem zadání funkce je tzv. [[rekurzivní funkce (matematika)|rekurzivní funkce]]. Zadání funkce rekurentně je zadání předpisu, který dává do vztahu nějaké hodnoty funkce s jinými hodnotami takovým způsobem, že funkce je dobře definována. | Zvláštním případem zadání funkce je tzv. [[rekurzivní funkce (matematika)|rekurzivní funkce]]. Zadání funkce rekurentně je zadání předpisu, který dává do vztahu nějaké hodnoty funkce s jinými hodnotami takovým způsobem, že funkce je dobře definována. | ||
| - | Příkladem takové funkce může být např. funkce definovaná na přirozených číslech, kterou definujeme vztahy < | + | Příkladem takové funkce může být např. funkce definovaná na přirozených číslech, kterou definujeme vztahy <big>\(f(0) = 1\)</big> a <big>\(f(n) = n \cdot f(n-1)\)</big> pro <big>\(n = 1,2,...\)</big>. Uvedenou funkci lze také zapsat jako <big>\(f(n) = n!\)</big>, tzn. tato funkce počítá [[faktoriál]]. |
Celý proces výpočtu rekurzivní funkce je označován jako [[rekurze]] a našel uplatnění především ve [[výpočetní technika|výpočetní technice]]. | Celý proces výpočtu rekurzivní funkce je označován jako [[rekurze]] a našel uplatnění především ve [[výpočetní technika|výpočetní technice]]. | ||
== Operace s funkcemi == | == Operace s funkcemi == | ||
| - | Mějme funkci < | + | Mějme funkci <big>\(f(x)\)</big> s [[definiční obor|definičním oborem]] <big>\(D_f(x)\)</big> a funkci <big>\(g(x)\)</big> s definičním oborem <big>\(D_g(x)\)</big>. Společný definiční obor obou funkcí je [[průnik]]em obou definičních oborů, tzn. <big>\(D = D_f \cap D_g\)</big>. |
| - | Funkce < | + | Funkce <big>\(f, g\)</big> jsou si na <big>\(D\)</big> rovny, pokud platí <big>\(f(x) = g(x)\)</big> pro všechna <big>\(x \in D\)</big>. |
| - | ''[[Sčítání|Součtem]] funkcí'' < | + | ''[[Sčítání|Součtem]] funkcí'' <big>\(f, g\)</big> na <big>\(D\)</big> označíme funkci <big>\(h\)</big> takovou, že <big>\(h(x) = f(x) + g(x)\)</big> pro všechna <big>\(x \in D\)</big>. |
| - | ''[[Násobení|Součinem]] funkcí'' < | + | ''[[Násobení|Součinem]] funkcí'' <big>\(f, g\)</big> na <big>\(D\)</big> označíme funkci <big>\(h\)</big> takovou, že <big>\(h(x) = f(x) \cdot g(x)\)</big> pro všechna <big>\(x \in D\)</big>. |
| - | ''[[Dělení|Podílem]] funkcí'' < | + | ''[[Dělení|Podílem]] funkcí'' <big>\(f, g\)</big> na <big>\(D^\prime\)</big> označíme funkci <big>\(h\)</big> takovou, že <big>\(h(x) = \frac{f(x)}{g(x)}\)</big> pro všechna <big>\(x \in D^\prime\)</big>, kde <big>\(D^\prime\)</big> je definiční obor <big>\(D\)</big>, z něhož byla vyňata všechna <big>\(x\)</big>, pro která platí <big>\(g(x) = 0\)</big>. |
== Související články == | == Související články == | ||
Aktuální verze z 14. 8. 2022, 14:51
Funkce je v matematice název pro zobrazení z nějaké množiny M do množiny čísel (většinou reálných nebo komplexních), nebo do vektorového prostoru (pak se mluví o vektorové funkci). Je to tedy předpis, který každému prvku z množiny M jednoznačně přiřadí nějaké číslo nebo vektor (hodnotu funkce). Někdy se však slovo funkce používá pro libovolné zobrazení.
Obsah |
Definice
Poněkud neformální
Na množině čísel M je definovaná funkce, je-li dán předpis, podle kterého je každému x náležícímu do množiny M přiřazeno právě jedno číslo y.
Značíme: \(y=f(x)\).
Proměnná \(x\) se označuje jako argument funkce (nezávisle proměnná). Proměnná \(y\) je funkční hodnota (závisle proměnná).
M nazýváme definičním oborem funkce. Pokud není při zadání funkce uveden definiční obor, pak se za definiční obor obvykle považuje množina všech hodnot nezávisle proměnné, pro něž má funkce smysl. Definičním oborem může být například množina celých, reálných nebo komplexních čísel. Definiční obor může mít i více dimenzí. Pokud má dvě, pak můžeme říkat, že má funkce dva argumenty, nebo že jejím argumentem je jeden dvourozměrný vektor. Jedná se o dva pohledy na stejnou věc. V případě, že má vektor, který je argumentem funkce, nekonečnou dimenzi (většinou nespočetnou), nemluvíme již o funkci, ale o funkcionálu.
Množinu všech čísel \(\ f(x)\), takových, že \(x \in\ M\), nazýváme oborem hodnot dané funkce.
Matematicky přesnější
Funkce \(f\) je podmnožina součinu \(M\times T\), kde M a T jsou množiny, T je obvykle podmnožina reálných nebo komplexních čísel, taková, že pro každý prvek m množiny M existuje nejvýše jedna uspořádaná dvojice \([m,x]\in f\). Obvykle píšeme \(f(m)=x\).
Definičním oborem funkce je pak podmnožina všech prvků množiny M, ke kterým taková uspořádaná dvojice existuje právě jedna. Říkáme, že pro prvky množiny M, které nejsou prvky definičního oboru, daná funkce není definována.
Oborem hodnot dané funkce je množina všech prvků x množiny T, ke kterým v relaci existuje alespoň jedna uspořádaná dvojice \([m,x]\in f\), kde \(m \in M\).
Způsoby zadání funkce
Analyticky
Analytickým předpisem rozumíme zadání funkce ve formě \(y = f(x)\), pak říkáme, že funkce je zadána explicitním vyjádřením (explicitní funkce). Funkci můžeme vyjádřit také v implicitním tvaru (implicitní funkce) jako \(F(x,y) = 0\). Dalším způsobem je zápis v parametrickém tvaru (parametrická funkce) soustavou rovnic \(x = f_1(t)\), \(y = f_2(t)\), kde \(t\) je vhodný parametr.
Příklad
Např. \(y = 2x^2\) je explicitní zápis kvadratické funkce. V implicitním tvaru lze stejnou rovnici zapsat jako \(y - 2x^2 = 0\). V parametrickém tvaru lze zvolit např. soustavu rovnic \(x = \frac{t}{\sqrt{2}}\), \(y = t^2\).
Graficky
Při grafickém zadání funkci vyjádříme grafem.
Příklad
Příklad zadání funkce grafem (\(D(x)\) označuje definiční obor a \(V(y)\) obor hodnot)
Tabulkou (výčtem hodnot)
Funkční předpis může být zadán také výčtem hodnot, který obvykle uspořádáme do tabulky.
Příklad
Příkladem může být např. zadání funkce
| \(x\) | 1 | 2 | 3 | 7 | 9 |
| \(y\) | 2 | 4 | 5 | 3 | 3 |
Definičním oborem je zde množina \(\{1,2,3,7,9\}\) a oborem hodnot je množina \(\{2,3,4,5\} \).
Typy funkcí
Je-li nezávisle proměnná z množiny reálných čísel, pak hovoříme o funkci reálné proměnné, pokud je nezávisle proměnná z množiny komplexních čísel, hovoříme o funkci komplexní proměnné. Pokud je závislá proměnná z množiny reálných čísel, pak s jedná o reálnou funkci, je-li z množiny komplexních čísel, jde o komplexní funkci. Např. komplexní funkce reálné proměnné přiřazuje každému reálnému číslu (z definičního oboru) komplexní číslo.
Argumentem funkce nemusí být jen čísla, ale mohou jím být také matice, vektory, tenzory, apod. Pak podle typu argumentu hovoříme o maticové funkci, vektorové funkci, tenzorové funkci, apod.
O funkci obsahující jedinou nezávisle proměnnou hovoříme jako o funkci jedné proměnné, např. \(y = f(x)\). Funkce obsahující dvě (nebo více) nezávislých proměnných pak označujeme jako funkci dvou (tří, čtyř, …) proměnných, např. \(z = f(x,y)\) je funkce dvou proměnných \(x\) a \(y\). Funkci \(n\)-proměnných zapisujeme jako
- \(f(x_1,x_2,..., x_n)\)
- \(f(x_i)\) pro \(i=1,2,...,n\)
- \(f(X)\), kde \(X = [x_1,x_2,...,x_n]\) představuje bod v n-rozměrném prostoru
- \(f(r)\), kde \(r\) představuje polohový vektor bodu v n-rozměrném prostoru.
Algebraická a transcendentní funkce
Funkci označujeme jako algebraickou, pokud ji lze vyjádřit ve tvaru polynomu, např. pokud lze funkci \(y = f(x)\) vyjádřit jako \(P(x,y) = 0\), kde \(P\) je polynom, pak se jedná o algebraickou funkci. Stupeň polynomu \(P\) pak určuje stupeň funkce. Funkce, které nejsou algebraické, označujeme jako transcendentní. Mezi transcendentní funkce se řadí funkce sin, cos, tg, cotg, exp, log, případně další, které nejdou vyjádřit pomocí elementárních funkcí.
Algebraické funkce lze dále rozdělit na racionální funkce a iracionální funkce. Iracionální funkce jsou funkce obsahující \(x^{\frac{m}{n}}\), kde \(m, n\) jsou nesoudělná čísla.
Transcendentní funkce lze rozdělit na nižší, kam patří např. exponenciální, logaritmické, goniometrické a cyklometrické funkce, a vyšší. Vyšší transcendentní funkce nelze pomocí elementárních funkcí vyjádřit v konečném tvaru.
Rekurzivní funkce
Zvláštním případem zadání funkce je tzv. rekurzivní funkce. Zadání funkce rekurentně je zadání předpisu, který dává do vztahu nějaké hodnoty funkce s jinými hodnotami takovým způsobem, že funkce je dobře definována.
Příkladem takové funkce může být např. funkce definovaná na přirozených číslech, kterou definujeme vztahy \(f(0) = 1\) a \(f(n) = n \cdot f(n-1)\) pro \(n = 1,2,...\). Uvedenou funkci lze také zapsat jako \(f(n) = n!\), tzn. tato funkce počítá faktoriál.
Celý proces výpočtu rekurzivní funkce je označován jako rekurze a našel uplatnění především ve výpočetní technice.
Operace s funkcemi
Mějme funkci \(f(x)\) s definičním oborem \(D_f(x)\) a funkci \(g(x)\) s definičním oborem \(D_g(x)\). Společný definiční obor obou funkcí je průnikem obou definičních oborů, tzn. \(D = D_f \cap D_g\).
Funkce \(f, g\) jsou si na \(D\) rovny, pokud platí \(f(x) = g(x)\) pro všechna \(x \in D\).
Součtem funkcí \(f, g\) na \(D\) označíme funkci \(h\) takovou, že \(h(x) = f(x) + g(x)\) pro všechna \(x \in D\).
Součinem funkcí \(f, g\) na \(D\) označíme funkci \(h\) takovou, že \(h(x) = f(x) \cdot g(x)\) pro všechna \(x \in D\).
Podílem funkcí \(f, g\) na \(D^\prime\) označíme funkci \(h\) takovou, že \(h(x) = \frac{f(x)}{g(x)}\) pro všechna \(x \in D^\prime\), kde \(D^\prime\) je definiční obor \(D\), z něhož byla vyňata všechna \(x\), pro která platí \(g(x) = 0\).
Související články
- Meromorfní funkce
- Obraz funkce
- Vzor funkce
- Průběh funkce
- Inverzní funkce
- Sudé a liché funkce
- Periodická funkce
- Skládání funkcí
- Komplexní funkce
- Prostá funkce
- Spojitá funkce
- Monotónní funkce
Externí odkazy
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |