Interpolace
Z Multimediaexpo.cz
m (Nahrazení textu „<math>“ textem „<big>\(“) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| Řádka 8: | Řádka 8: | ||
== Definice == | == Definice == | ||
[[Soubor: Interpolation example polynomial.png|thumb|220px| Interpolace polynomem 6. stupně ]] | [[Soubor: Interpolation example polynomial.png|thumb|220px| Interpolace polynomem 6. stupně ]] | ||
| - | Mějme funkci f(x), jejíž hodnota je známa v bodech <big>\(f(x_0)</ | + | Mějme funkci f(x), jejíž hodnota je známa v bodech <big>\(f(x_0)\)</big>, <big>\(f(x_1)\)</big>, ... <big>\(f(x_n)\)</big>. Interpolace znamená nalezení funkční hodnoty <big>\(f(x)\)</big>, pokud platí, že <big>\(x_0\)</big> < <big>\(x\)</big> < <big>\(x_n\)</big>. |
== Interpolační křivka == | == Interpolační křivka == | ||
| - | Někdy se interpolací rozumí proložení bodů <big>\(f(x_0)</ | + | Někdy se interpolací rozumí proložení bodů <big>\(f(x_0)\)</big>, <big>\(f(x_1)\)</big>, ... <big>\(f(x_n)\)</big> analytickou křivkou, která pak umožňuje jednoduchý výpočet funkčních hodnot ve všech mezilehlých bodech. Podle počtu známých bodů n se pak nejčastěji používá: |
* pro n = 2 lineární interpolace (přímkou) | * pro n = 2 lineární interpolace (přímkou) | ||
* pro n = 3 kvadratická interpolace (parabolou nebo kružnicí) | * pro n = 3 kvadratická interpolace (parabolou nebo kružnicí) | ||
| Řádka 21: | Řádka 21: | ||
Pro | Pro | ||
| - | <big>\(x_0</ | + | <big>\(x_0\)</big> < <big>\(x_i\)</big> < <big>\(x_1\)</big> |
platí, že | platí, že | ||
| - | <big>\(f(x) = f_0 + {{f_1-f_0}\over{x_1-x_0}}\,(x-x_0)</ | + | <big>\(f(x) = f_0 + {{f_1-f_0}\over{x_1-x_0}}\,(x-x_0)\)</big>. |
== Související články == | == Související články == | ||
Aktuální verze z 14. 8. 2022, 14:52
Interpolace (lat. inter-polare, vylepšit vkládáním) v numerické matematice znamená nalezení přibližné hodnoty funkce v nějakém intervalu, je-li její hodnota známa jen v některých jiných bodech tohoto intervalu. Používá se v případě, že hodnoty funkce v určitých bodech intervalu jsou buďto uvedeny v tabulce, anebo získány měřením.
Podobného původu je i slovo extrapolace, které označuje nalézání přibližné hodnoty funkce mimo interval známých hodnot, což je méně spolehlivé. Užívá se nejčastěji pro odhady tendencí do budoucnosti, například cen v ekonomii.
Od aproximace se interpolace liší tím, že hledaná křivka přesně prochází všemi známými (změřenými) body.
Obsah |
Definice
Mějme funkci f(x), jejíž hodnota je známa v bodech \(f(x_0)\), \(f(x_1)\), ... \(f(x_n)\). Interpolace znamená nalezení funkční hodnoty \(f(x)\), pokud platí, že \(x_0\) < \(x\) < \(x_n\).
Interpolační křivka
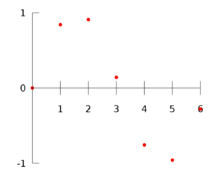
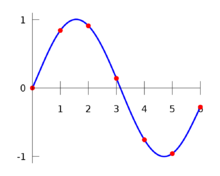
Někdy se interpolací rozumí proložení bodů \(f(x_0)\), \(f(x_1)\), ... \(f(x_n)\) analytickou křivkou, která pak umožňuje jednoduchý výpočet funkčních hodnot ve všech mezilehlých bodech. Podle počtu známých bodů n se pak nejčastěji používá:
- pro n = 2 lineární interpolace (přímkou)
- pro n = 3 kvadratická interpolace (parabolou nebo kružnicí)
- pro n > 3 interpolace polynomem n-tého stupně; pro výpočet koeficientů tohoto polynomu se nejčastěji požívá Čebyševova metoda.
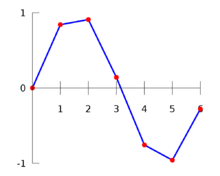
Lineární interpolace
Nejjednodušší a nejčastěji používaná lineární interpolace (někdy také interpolace lineárním splajnem) spočívá v proložení dvou sousedních bodů přímkou; zavedl ji Isaac Newton. (Nezaměňovat s Newtonovou interpolací)
Pro \(x_0\) < \(x_i\) < \(x_1\) platí, že \(f(x) = f_0 + {{f_1-f_0}\over{x_1-x_0}}\,(x-x_0)\).
Související články
- Lagrangeova interpolace
- Newtonova interpolace
- Aproximace
- Geometrie
- Modelování křivek
- Křivka
- Numerická matematika
- Taylorova řada
Literatura
- Stručný statistický slovník. Praha 1967, heslo Interpolace, str. 82
Externí odkazy
|
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |