Multimediaexpo.cz je již 18 let na českém internetu !!
Algoritmus de Casteljau
Z Multimediaexpo.cz
m (1 revizi) |
(+ Aktualizace) |
||
| (Není zobrazena jedna mezilehlá verze.) | |||
| Řádka 1: | Řádka 1: | ||
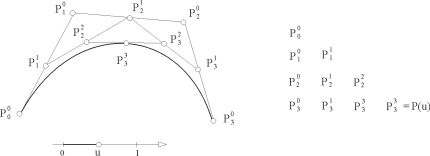
| - | + | '''De Casteljauův algoritmus''' se používá pro výpočet bodu na [[Bézierova křivka|Bézierově křivce]]. | |
| + | [[Soubor:Výpočet_bodu_na_Bézierově_kubice_pomocí_algoritmu_de_Casteljau.JPG|Výpočet bodu]] | ||
| + | [[Soubor:ZvyseniStupneCasteljau.JPG|thumb|230px|Náčrt]] | ||
| + | [[Soubor:bezier_koefs.jpg|thumb|230px|Racionální algoritmus de Casteljau]] | ||
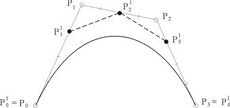
| + | Když si výpočet graficky znázorníme (viz obrázek), zjistíme, že se ve skutečnosti nejedná o nic jiného, než o postupné dělení [[úsečka|úseček]] řídícího [[mnohoúhelník|polygonu]] v zadaném poměru. Počet nově vzniklých bodů se v každém kroku zmenšuje o 1 a ve chvíli, kdy zůstane bod jediný, dostaneme hledaný bod křivky. | ||
| + | Bod na Bézierově křivce můžeme rovněž vypočítat přímo pomocí [[vektorová rovnice|vektorové rovnice]] Bézierovy křivky, kdy použijeme algoritmus pro výpočet Bernsteinových polynomů. | ||
| + | Více informací o křivkách najdete v [[Geometrie|geometrii]]. | ||
| + | |||
| + | == Racionální de Casteljauův algoritmus == | ||
| + | Racionální de Casteljauův algoritmus je metoda pro výpočet [[bod]]u na racionální Bézierově [[křivka|křivce]], která je rozšířením de Casteljauova algoritmu. Jediným rozdílem oproti němu je, že do výpočtu zahrnujeme váhové parametry, a pro každý nový bod spočítáme jeho poměrnou váhu vzhledem k bodům předešlým. | ||
| + | |||
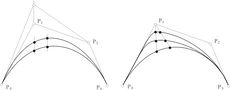
| + | Pomocí váhových koeficientů lze měnit tvar racionální [[Bézierova křivka|Bézierovy křivky]], s rostoucím váhovým [[koeficient]]em se křivka k danému bodu „přibližuje“, jak je vidět na následujícím obrázku. | ||
| + | |||
| + | == Externí odkazy == | ||
| + | |||
| + | {{Commonscat|De Casteljau's algorithm}}{{Článek z Wikipedie}} | ||
[[Kategorie:Algoritmy]] | [[Kategorie:Algoritmy]] | ||
[[Kategorie:Geometrie]] | [[Kategorie:Geometrie]] | ||
Aktuální verze z 29. 5. 2023, 16:04
De Casteljauův algoritmus se používá pro výpočet bodu na Bézierově křivce.
Když si výpočet graficky znázorníme (viz obrázek), zjistíme, že se ve skutečnosti nejedná o nic jiného, než o postupné dělení úseček řídícího polygonu v zadaném poměru. Počet nově vzniklých bodů se v každém kroku zmenšuje o 1 a ve chvíli, kdy zůstane bod jediný, dostaneme hledaný bod křivky. Bod na Bézierově křivce můžeme rovněž vypočítat přímo pomocí vektorové rovnice Bézierovy křivky, kdy použijeme algoritmus pro výpočet Bernsteinových polynomů. Více informací o křivkách najdete v geometrii.
Racionální de Casteljauův algoritmus
Racionální de Casteljauův algoritmus je metoda pro výpočet bodu na racionální Bézierově křivce, která je rozšířením de Casteljauova algoritmu. Jediným rozdílem oproti němu je, že do výpočtu zahrnujeme váhové parametry, a pro každý nový bod spočítáme jeho poměrnou váhu vzhledem k bodům předešlým.
Pomocí váhových koeficientů lze měnit tvar racionální Bézierovy křivky, s rostoucím váhovým koeficientem se křivka k danému bodu „přibližuje“, jak je vidět na následujícím obrázku.
Externí odkazy
|
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |