The English encyclopedia Allmultimedia.org will be launched in two phases.
The final launch of the Allmultimedia.org will take place on February 27, 2026
(shortly after the 2026 Winter Olympics).

Polární soustava souřadnic

Z Multimediaexpo.cz

(Rozdíly mezi verzemi)
m (1 revizi)
m (Nahrazení textu „<math>“ textem „<big>\(“)
Řádka 1: Řádka 1:
-
'''Polární soustava souřadnic''' je taková [[soustava souřadnic]] v [[rovina|rovině]], u které jedna souřadnice (označovaná <math>r</math>) udává [[vzdálenost]] [[bod]]u od počátku souřadnic, druhá souřadnice (označovaná <math>\varphi</math>) udává [[úhel]] spojnice tělesa a počátku od zvolené osy ležící v rovině (nejčastěji jí odpovídá osa <math>x</math> [[Kartézská soustava souřadnic|kartézských souřadnic]]). Jedná se o [[Ortogonální souřadnicová soustava|ortogonální soustavu souřadnic]] s [[Lamého koeficienty]]
+
'''Polární soustava souřadnic''' je taková [[soustava souřadnic]] v [[rovina|rovině]], u které jedna souřadnice (označovaná <big>\(r</math>) udává [[vzdálenost]] [[bod]]u od počátku souřadnic, druhá souřadnice (označovaná <big>\(\varphi</math>) udává [[úhel]] spojnice tělesa a počátku od zvolené osy ležící v rovině (nejčastěji jí odpovídá osa <big>\(x</math> [[Kartézská soustava souřadnic|kartézských souřadnic]]). Jedná se o [[Ortogonální souřadnicová soustava|ortogonální soustavu souřadnic]] s [[Lamého koeficienty]]
-
<math>h_r = 1 \quad h_{\varphi} = r</math>.
+
<big>\(h_r = 1 \quad h_{\varphi} = r</math>.
Polární soustava souřadnic je vhodná v případech takových [[Mechanický pohyb|pohybů]], při nichž se nemění vzdálenost tělesa od jednoho bodu (počátku souřadnic), například u [[Pohyb po kružnici|pohybu po kružnici]], případně se tato vzdálost mění s nějakou jednoduchou závislostí.
Polární soustava souřadnic je vhodná v případech takových [[Mechanický pohyb|pohybů]], při nichž se nemění vzdálenost tělesa od jednoho bodu (počátku souřadnic), například u [[Pohyb po kružnici|pohybu po kružnici]], případně se tato vzdálost mění s nějakou jednoduchou závislostí.
Řádka 11: Řádka 11:
[[Transformace souřadnic|Transformace]] '''polárních souřadnic''' na [[Kartézská soustava souřadnic|kartézské]]:<br />
[[Transformace souřadnic|Transformace]] '''polárních souřadnic''' na [[Kartézská soustava souřadnic|kartézské]]:<br />
-
:<math>x = r \cos{\varphi}\,</math><br />
+
:<big>\(x = r \cos{\varphi}\,</math><br />
-
:<math>y = r \sin{\varphi}\,</math><br />
+
:<big>\(y = r \sin{\varphi}\,</math><br />
Převod [[Kartézská soustava souřadnic|kartézských souřadnic]] na '''polární''':<br />
Převod [[Kartézská soustava souřadnic|kartézských souřadnic]] na '''polární''':<br />
-
:<math>r = \sqrt{x^2 + y^2}</math><br />
+
:<big>\(r = \sqrt{x^2 + y^2}</math><br />
-
:<math>\varphi = \operatorname{arctg}\left(\frac{y}{x}\right)</math><br />
+
:<big>\(\varphi = \operatorname{arctg}\left(\frac{y}{x}\right)</math><br />
-
Tato převodní funkce však funguje jen na [[interval (matematika)|intervalu]] <math>\varphi \in \langle 0,\frac{\pi}{2}\rangle</math> - pro jiné intervaly bychom museli změnit znaménko [[Arkus tangens|funkce arctg(''x'')]]. Abychom mohli popsat [[inverzní funkce|inverzi]] pro daný úhel na celém jeho [[definiční obor|definičním intervalu]], bývá často používána funkce [[funkce arctg2|arctg2(''y'',''x'')]] definovaná jako
+
Tato převodní funkce však funguje jen na [[interval (matematika)|intervalu]] <big>\(\varphi \in \langle 0,\frac{\pi}{2}\rangle</math> - pro jiné intervaly bychom museli změnit znaménko [[Arkus tangens|funkce arctg(''x'')]]. Abychom mohli popsat [[inverzní funkce|inverzi]] pro daný úhel na celém jeho [[definiční obor|definičním intervalu]], bývá často používána funkce [[funkce arctg2|arctg2(''y'',''x'')]] definovaná jako
-
:<math>\operatorname{arctg2}(y,x) = \left\{\begin{matrix}  
+
:<big>\(\operatorname{arctg2}(y,x) = \left\{\begin{matrix}  
\operatorname{arctg}\left(\frac{y}{x}\right),\ \ \ \ \ \ & \mbox{je-li } (x>0) \wedge (y>0), \\  
\operatorname{arctg}\left(\frac{y}{x}\right),\ \ \ \ \ \ & \mbox{je-li } (x>0) \wedge (y>0), \\  
\operatorname{arctg}\left(\frac{y}{x}\right) + \pi,\ & \mbox{je-li }  
\operatorname{arctg}\left(\frac{y}{x}\right) + \pi,\ & \mbox{je-li }  
Řádka 28: Řádka 28:
Převod [[Kartézská soustava souřadnic|kartézských souřadnic]] na '''polární''' má potom zápis:
Převod [[Kartézská soustava souřadnic|kartézských souřadnic]] na '''polární''' má potom zápis:
-
:<math>r = \sqrt{x^2 + y^2}</math><br />
+
:<big>\(r = \sqrt{x^2 + y^2}</math><br />
-
:<math>\varphi = \operatorname{arctg2}\left(y,x\right)</math><br />
+
:<big>\(\varphi = \operatorname{arctg2}\left(y,x\right)</math><br />
== Metrické vlastnosti ==
== Metrické vlastnosti ==
Řádka 35: Řádka 35:
Délka [[Infinitezimální hodnota|infinitesimální]] úsečky se spočte jako
Délka [[Infinitezimální hodnota|infinitesimální]] úsečky se spočte jako
-
:<math>\mathrm{d}s^2=\mathrm{d}r^2+r^2\mathrm{d}\varphi^2,</math>
+
:<big>\(\mathrm{d}s^2=\mathrm{d}r^2+r^2\mathrm{d}\varphi^2,</math>
tedy délka [[křivka|křivky]] obecně jako
tedy délka [[křivka|křivky]] obecně jako
-
:<math>\int_{t_1}^{t_2}{\sqrt{\left(\frac{\mathrm{d}r(t)}{\mathrm{d}t}\right)^2
+
:<big>\(\int_{t_1}^{t_2}{\sqrt{\left(\frac{\mathrm{d}r(t)}{\mathrm{d}t}\right)^2
             +r^2\left(\frac{\mathrm{d}\varphi(t)}{\mathrm{d}t}\right)^2}}\mathrm{d}t,</math>
             +r^2\left(\frac{\mathrm{d}\varphi(t)}{\mathrm{d}t}\right)^2}}\mathrm{d}t,</math>
-
kde ''t'' je parametr dané křivky a s je její délka od <math>t_1</math> do <math>t_2</math>.
+
kde ''t'' je parametr dané křivky a s je její délka od <big>\(t_1</math> do <big>\(t_2</math>.
[[Obsah]] infinitesimálního elementu plochy spočteme jako
[[Obsah]] infinitesimálního elementu plochy spočteme jako
-
:<math>\mathrm{d}S=r \mathrm{d}r\mathrm{d}\varphi,</math>
+
:<big>\(\mathrm{d}S=r \mathrm{d}r\mathrm{d}\varphi,</math>
takže celkový obsah spočteme [[integrál|integrací]] tohoto výrazu přes danou oblast vyjádřenou v polárních souřadnicích.
takže celkový obsah spočteme [[integrál|integrací]] tohoto výrazu přes danou oblast vyjádřenou v polárních souřadnicích.
Řádka 52: Řádka 52:
[[Afinní konexe]] jsou dány vztahy
[[Afinní konexe]] jsou dány vztahy
-
:<math>{\Gamma^r}_{rr}={\Gamma^\varphi}_{\varphi\varphi}=
+
:<big>\({\Gamma^r}_{rr}={\Gamma^\varphi}_{\varphi\varphi}=
{\Gamma^r}_{r\varphi}={\Gamma^r}_{\varphi r}={\Gamma^\varphi}_{rr}=0</math>
{\Gamma^r}_{r\varphi}={\Gamma^r}_{\varphi r}={\Gamma^\varphi}_{rr}=0</math>
-
:<math>{\Gamma^\varphi}_{\varphi r}={\Gamma^\varphi}_{r \varphi} = \frac{1}{r}</math>
+
:<big>\({\Gamma^\varphi}_{\varphi r}={\Gamma^\varphi}_{r \varphi} = \frac{1}{r}</math>
-
:<math>{\Gamma^r}_{\varphi \varphi}= -r</math>
+
:<big>\({\Gamma^r}_{\varphi \varphi}= -r</math>
== Diferenciální operátory v polárních souřadnicích ==
== Diferenciální operátory v polárních souřadnicích ==
-
:<math>\nabla f =  
+
:<big>\(\nabla f =  
{\partial f \over \partial r }\boldsymbol{\hat r }  
{\partial f \over \partial r }\boldsymbol{\hat r }  
   + {1 \over  r }{\partial f \over \partial \varphi}\boldsymbol{\hat \varphi}  
   + {1 \over  r }{\partial f \over \partial \varphi}\boldsymbol{\hat \varphi}  
Řádka 65: Řádka 65:
-
:<math>\nabla \cdot \mathbf{A} =
+
:<big>\(\nabla \cdot \mathbf{A} =
{1 \over r }{\partial \left( r A_r \right) \over \partial r }  
{1 \over r }{\partial \left( r A_r \right) \over \partial r }  
   + {1 \over  r }{\partial A_\varphi \over \partial \varphi}  
   + {1 \over  r }{\partial A_\varphi \over \partial \varphi}  
Řádka 71: Řádka 71:
-
:<math>\Delta f = \nabla^2 f =  
+
:<big>\(\Delta f = \nabla^2 f =  
{1 \over r }{\partial \over \partial r }\left( r {\partial f \over \partial r }\right)  
{1 \over r }{\partial \over \partial r }\left( r {\partial f \over \partial r }\right)  
   + {1 \over  r ^2}{\partial^2 f \over \partial \varphi^2}  
   + {1 \over  r ^2}{\partial^2 f \over \partial \varphi^2}  
Řádka 77: Řádka 77:
-
:<math>\Delta \mathbf{A} =  
+
:<big>\(\Delta \mathbf{A} =  
   \left(\Delta A_r  - {A_r  \over  r ^2}  
   \left(\Delta A_r  - {A_r  \over  r ^2}  
     - {2 \over  r ^2}{\partial A_\varphi \over \partial \varphi}\right) \boldsymbol{\hat r }  +  
     - {2 \over  r ^2}{\partial A_\varphi \over \partial \varphi}\right) \boldsymbol{\hat r }  +  

Verze z 14. 8. 2022, 14:49

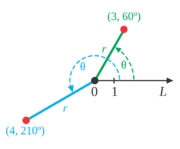
Polární soustava souřadnic je taková soustava souřadnic v rovině, u které jedna souřadnice (označovaná \(r</math>) udává vzdálenost bodu od počátku souřadnic, druhá souřadnice (označovaná \(\varphi</math>) udává úhel spojnice tělesa a počátku od zvolené osy ležící v rovině (nejčastěji jí odpovídá osa \(x</math> kartézských souřadnic). Jedná se o ortogonální soustavu souřadnic s Lamého koeficienty

\(h_r = 1 \quad h_{\varphi} = r</math>.

Polární soustava souřadnic je vhodná v případech takových pohybů, při nichž se nemění vzdálenost tělesa od jednoho bodu (počátku souřadnic), například u pohybu po kružnici, případně se tato vzdálost mění s nějakou jednoduchou závislostí.

Souřadnicová síť v polárních souřadnicích
Bod v polární soustavě souřadnic
Ukázka dvou bodů v polárních souřadnicích: [r=3; φ=60°] a [r=4; φ=210°]
Ukázka převodu polárních souřadnic [r; φ] na kartézské [x; y]

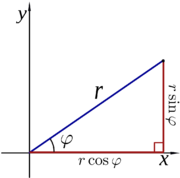
Transformace polárních souřadnic na kartézské:

\(x = r \cos{\varphi}\,</math>
\(y = r \sin{\varphi}\,</math>

Převod kartézských souřadnic na polární:

\(r = \sqrt{x^2 + y^2}</math>
\(\varphi = \operatorname{arctg}\left(\frac{y}{x}\right)</math>

Tato převodní funkce však funguje jen na intervalu \(\varphi \in \langle 0,\frac{\pi}{2}\rangle</math> - pro jiné intervaly bychom museli změnit znaménko funkce arctg(x). Abychom mohli popsat inverzi pro daný úhel na celém jeho definičním intervalu, bývá často používána funkce arctg2(y,x) definovaná jako

\(\operatorname{arctg2}(y,x) = \left\{\begin{matrix}

\operatorname{arctg}\left(\frac{y}{x}\right),\ \ \ \ \ \ & \mbox{je-li } (x>0) \wedge (y>0), \\ \operatorname{arctg}\left(\frac{y}{x}\right) + \pi,\ & \mbox{je-li } (x<0), \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \operatorname{arctg}\left(\frac{y}{x}\right) + 2\pi, & \mbox{je-li } (x>0) \wedge (y<0), \\ \end{matrix}\right.</math>

Převod kartézských souřadnic na polární má potom zápis:

\(r = \sqrt{x^2 + y^2}</math>
\(\varphi = \operatorname{arctg2}\left(y,x\right)</math>

Metrické vlastnosti

Délka infinitesimální úsečky se spočte jako

\(\mathrm{d}s^2=\mathrm{d}r^2+r^2\mathrm{d}\varphi^2,</math>

tedy délka křivky obecně jako

\(\int_{t_1}^{t_2}{\sqrt{\left(\frac{\mathrm{d}r(t)}{\mathrm{d}t}\right)^2 
           +r^2\left(\frac{\mathrm{d}\varphi(t)}{\mathrm{d}t}\right)^2}}\mathrm{d}t,</math>

kde t je parametr dané křivky a s je její délka od \(t_1</math> do \(t_2</math>.

Obsah infinitesimálního elementu plochy spočteme jako

\(\mathrm{d}S=r \mathrm{d}r\mathrm{d}\varphi,</math>

takže celkový obsah spočteme integrací tohoto výrazu přes danou oblast vyjádřenou v polárních souřadnicích.

Afinní konexe jsou dány vztahy

\({\Gamma^r}_{rr}={\Gamma^\varphi}_{\varphi\varphi}=

{\Gamma^r}_{r\varphi}={\Gamma^r}_{\varphi r}={\Gamma^\varphi}_{rr}=0</math>

\({\Gamma^\varphi}_{\varphi r}={\Gamma^\varphi}_{r \varphi} = \frac{1}{r}</math>
\({\Gamma^r}_{\varphi \varphi}= -r</math>

Diferenciální operátory v polárních souřadnicích

\(\nabla f =

{\partial f \over \partial r }\boldsymbol{\hat r } 

 + {1 \over  r }{\partial f \over \partial \varphi}\boldsymbol{\hat \varphi}

</math>


\(\nabla \cdot \mathbf{A} =

{1 \over r }{\partial \left( r A_r \right) \over \partial r } 

 + {1 \over  r }{\partial A_\varphi \over \partial \varphi}

</math>


\(\Delta f = \nabla^2 f =

{1 \over r }{\partial \over \partial r }\left( r {\partial f \over \partial r }\right) 

 + {1 \over  r ^2}{\partial^2 f \over \partial \varphi^2}

</math>


\(\Delta \mathbf{A} = 
 \left(\Delta A_r  - {A_r  \over  r ^2} 
   - {2 \over  r ^2}{\partial A_\varphi \over \partial \varphi}\right) \boldsymbol{\hat r }  + 
 \left(\Delta A_\varphi - {A_\varphi \over  r ^2} 
   + {2 \over  r ^2}{\partial A_r  \over \partial \varphi}\right) \boldsymbol{\hat\varphi}

</math>


Externí odkazy

Citováno z „http://ww.multimediaexpo.cz/mmecz/index.php/Pol%C3%A1rn%C3%AD_soustava_sou%C5%99adnic“