Kartézská soustava souřadnic
Z Multimediaexpo.cz
m (1 revizi) |
(+ Výrazné vylepšení) |
||
| Řádka 1: | Řádka 1: | ||
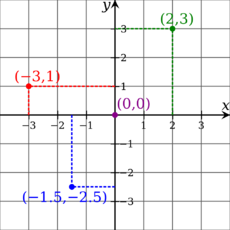
| + | [[Soubor:Cartesian-coordinate-system.png|thumb|230px|Body v rovinné kartézské soustavě souřadnic]] | ||
| + | [[Soubor:Prostorova_kartezska_soustava_souradnic.png|thumb|230px|Bod v prostorové pravotočivé kartézské soustavě souřadnic]] | ||
'''Kartézská soustava souřadnic''' je taková [[soustava souřadnic]], u které jsou souřadné osy vzájemně kolmé a protínají se v jednom bodě - počátku soustavy souřadnic. Jednotka se obvykle volí na všech osách stejně velká. Jednotlivé souřadnice polohy tělesa je možno dostat jako kolmé průměty polohy k jednotlivým osám. | '''Kartézská soustava souřadnic''' je taková [[soustava souřadnic]], u které jsou souřadné osy vzájemně kolmé a protínají se v jednom bodě - počátku soustavy souřadnic. Jednotka se obvykle volí na všech osách stejně velká. Jednotlivé souřadnice polohy tělesa je možno dostat jako kolmé průměty polohy k jednotlivým osám. | ||
| - | Soustava je pojmenována podle francouzského filosofa | + | Soustava je pojmenována podle francouzského filosofa René Descarta, který se zasloužil (kromě jiného) o propojení [[algebra|algebry]] a [[euklidovská geometrie|eukleidovské geometrie]]. |
V prostoru má kartézská soustava souřadnic 3 vzájemně kolmé osy (běžně označované x, y, z), v rovině 2 kolmé osy (x, y). | V prostoru má kartézská soustava souřadnic 3 vzájemně kolmé osy (běžně označované x, y, z), v rovině 2 kolmé osy (x, y). | ||
| - | |||
| - | |||
| - | |||
==Pravotočivá a levotočivá soustava prostorových kartézských souřadnic== | ==Pravotočivá a levotočivá soustava prostorových kartézských souřadnic== | ||
| - | Představte si, že v místě, kde stojíte, je počátek prostorové kartézské soustavy. Osa ''x'' nechť směřuje přímo vpřed (směrem, kterým se díváte), osa ''y'' nechť směřuje vlevo a osa ''z'' nechť směřuje vzhůru. Taková soustava se nazývá '''pravotočivá souřadná soustava'''. Příklad pravotočivé soustavy je na | + | Představte si, že v místě, kde stojíte, je počátek prostorové kartézské soustavy. Osa ''x'' nechť směřuje přímo vpřed (směrem, kterým se díváte), osa ''y'' nechť směřuje vlevo a osa ''z'' nechť směřuje vzhůru. Taková soustava se nazývá '''pravotočivá souřadná soustava'''. Příklad pravotočivé soustavy je na obrázku (dole). |
Určení, zda je soustava pravotočivá či levotočivá, usnadňuje [[pravidlo pravé ruky]]. | Určení, zda je soustava pravotočivá či levotočivá, usnadňuje [[pravidlo pravé ruky]]. | ||
| Řádka 19: | Řádka 18: | ||
== Externí odkazy == | == Externí odkazy == | ||
| - | {{Článek z Wikipedie}} | + | {{Commonscat|Coordinate systems}}{{Článek z Wikipedie}} |
[[Kategorie:Soustavy souřadnic]] | [[Kategorie:Soustavy souřadnic]] | ||
Aktuální verze z 7. 8. 2017, 12:55
Kartézská soustava souřadnic je taková soustava souřadnic, u které jsou souřadné osy vzájemně kolmé a protínají se v jednom bodě - počátku soustavy souřadnic. Jednotka se obvykle volí na všech osách stejně velká. Jednotlivé souřadnice polohy tělesa je možno dostat jako kolmé průměty polohy k jednotlivým osám.
Soustava je pojmenována podle francouzského filosofa René Descarta, který se zasloužil (kromě jiného) o propojení algebry a eukleidovské geometrie.
V prostoru má kartézská soustava souřadnic 3 vzájemně kolmé osy (běžně označované x, y, z), v rovině 2 kolmé osy (x, y).
Pravotočivá a levotočivá soustava prostorových kartézských souřadnic
Představte si, že v místě, kde stojíte, je počátek prostorové kartézské soustavy. Osa x nechť směřuje přímo vpřed (směrem, kterým se díváte), osa y nechť směřuje vlevo a osa z nechť směřuje vzhůru. Taková soustava se nazývá pravotočivá souřadná soustava. Příklad pravotočivé soustavy je na obrázku (dole).
Určení, zda je soustava pravotočivá či levotočivá, usnadňuje pravidlo pravé ruky.
Zaměníme-li osy x a y, získáme souřadnou soustavu levotočivou.
Obvykle se pracuje s pravotočivou souřadnou soustavou.
Externí odkazy
|
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |