Jednotková kružnice

Z Multimediaexpo.cz

(Rozdíly mezi verzemi)

Aktuální verze z 14. 8. 2022, 14:52

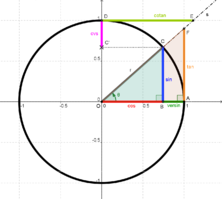
Jednotková kružnice: sinus, cosinus a tangens

Jednotková kružnice s hodnotami sin a cos

Jednotková kružnice je kružnice se středem v počátku souřadnic a o poloměru 1 používaná v matematice pro definici např. goniometrických funkcí.

Jejím zobecněním do vyšších rozměrů je jednotková koule.

Goniometrické funkce

Výhoda jednotkové kružnice spočívá v tom, že goniometrické funkce jsou definovány poměry a číslo 1 se v poměrech neprojevuje (1 * a = a) nebo vytváří nepřímou úměrnost (1/a). Neprojeví se ani souřadnice jejího středu, protože leží v počátku [0,0]. Její rovnice je tudíž velice jednoduchá:

x² + y² = 1

Souřadnice bodů na jednotkové kružnici pak přímo udávají hodnoty funkcí sin a cos pro úhly, které jejich průvodiče svírají s kladnou poloosou x: x = cos φ a y = sin φ. Protože absolutní hodnoty těchto funkcí se po 180° opakují a pro úhly φ z intervalu 90-180° platí, že f(φ)=f(180°-φ), stačí je tabelovat jen pro interval 0-90° a jejich znaménka pak udává následující tabulka:

	α	sin α	cos α	tg α	cotg α
1. kvadrant	0–90°	+	+	+	+
2. kvadrant	90–180°	+	−	−	−
3. kvadrant	180–270°	−	−	+	+
4. kvadrant	270–360°	−	+	−	−

Periodičnost

Na jednotkové kružnici lze také sledovat tzv. periodu: bod A může po kružnici obíhat zcela libovolně, a to i několikrát, takže jeho průvodič (polopřímkaSA) může s kladnou poloosou x svírat nekonečně mnoho úhlů, jež se od sebe liší o 2π čili o 360⁰.

Tak se s polopřímkou svírající s kladnou poloosou x úhel \(\frac{\pi}{3}\) (tj. 60°) budou překrývat i polopřímky s úhly \(\frac{7 \pi}{3}\) (420°), \(\frac{13 \pi}{3}\) (780°), \(-\frac{5 \pi}{3}\) (-300°) nebo \(-\frac{13 \pi}{3}\) (-780°).

Na tom se zakládá periodičnost goniometrických funkcí.

Související články

Externí odkazy

Commons nabízí fotografie, obrázky a videa k tématu
Jednotková kružnice

Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010
Informace o článku. Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. Tento text je dostupný za podmínek Creative Commons 3.0 Unported – creativecommons.org. Originální článek na české Wikipedii

@@ Řádka 25: / Řádka 25: @@
 Na jednotkové kružnici lze také sledovat tzv. [[perioda (matematika)|periodu]]: bod A může po kružnici obíhat zcela libovolně, a to i několikrát, takže jeho průvodič ([[polopřímka]]SA) může s kladnou [[poloosa|poloosou]] ''x'' svírat nekonečně mnoho úhlů, jež se od sebe liší o 2π čili o 360<sup>0</sup>.
-Tak se s polopřímkou svírající s kladnou poloosou ''x'' [[úhel]] <big>\(\frac{\pi}{3}</math> (tj. 60°) budou překrývat i polopřímky s úhly <big>\(\frac{7 \pi}{3}</math> (420°), <big>\(\frac{13 \pi}{3}</math> (780°), <big>\(-\frac{5 \pi}{3}</math> (-300°) nebo <big>\(-\frac{13 \pi}{3}</math> (-780°).
+Tak se s polopřímkou svírající s kladnou poloosou ''x'' [[úhel]] <big>\(\frac{\pi}{3}\)</big> (tj. 60°) budou překrývat i polopřímky s úhly <big>\(\frac{7 \pi}{3}\)</big> (420°), <big>\(\frac{13 \pi}{3}\)</big> (780°), <big>\(-\frac{5 \pi}{3}\)</big> (-300°) nebo <big>\(-\frac{13 \pi}{3}\)</big> (-780°).
 Na tom se zakládá periodičnost [[Goniometrická funkce|goniometrických funkcí]].