Vážení zákazníci a čtenáři – od 28. prosince do 2. ledna máme zavřeno.
Přejeme Vám krásné svátky a 52 týdnů pohody a štěstí v roce 2025 !

C1 kubická interpolace

Z Multimediaexpo.cz

(Rozdíly mezi verzemi)
m (1 revizi)
(+ Masivní vylepšení)
 
Řádka 1: Řádka 1:
-
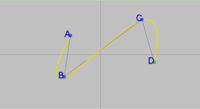
{{Wikipedia-cs|C1 kubická interpolace|700}}
+
[[Soubor:C1interKrivka.png|thumb|200px|Příklad užití C1 kubické křivky]]
 +
'''C1 kubická [[interpolace]]''' patří do skupiny interpolací křivek po obloucích, tj. každý úsek mezi dvěma opěrnými body se interpoluje zvlášť. Každý úsek C1 interpolační křivky bude kubický [[polynom]] vypočtený pomocí kubické Hermitovy interpolace. Pro C1 interpolační křivku musí být zabezpečena C1 [[spojitost]]. Tzn. v každém opěrném bodě mají sousední křivky stejný tečný [[vektor]]. (Zatímco u [[C2 kubická interpolace|C2 kubické interpolace]] je požadována i spojitost první [[derivace]] tečného vektoru.) K tomu potřebujeme tečné vektory v opěrných bodech vypočítat.
 +
== Související články==
 +
* [[křivka]]
 +
* [[geometrie]]
 +
 +
== Externí odkazy ==
 +
 +
 +
{{Článek z Wikipedie}}
[[Kategorie:Geometrie]]
[[Kategorie:Geometrie]]

Aktuální verze z 31. 8. 2014, 10:14

Příklad užití C1 kubické křivky

C1 kubická interpolace patří do skupiny interpolací křivek po obloucích, tj. každý úsek mezi dvěma opěrnými body se interpoluje zvlášť. Každý úsek C1 interpolační křivky bude kubický polynom vypočtený pomocí kubické Hermitovy interpolace. Pro C1 interpolační křivku musí být zabezpečena C1 spojitost. Tzn. v každém opěrném bodě mají sousední křivky stejný tečný vektor. (Zatímco u C2 kubické interpolace je požadována i spojitost první derivace tečného vektoru.) K tomu potřebujeme tečné vektory v opěrných bodech vypočítat.

Související články

Externí odkazy

Citováno z „http://ww.multimediaexpo.cz/mmecz/index.php/C1_kubick%C3%A1_interpolace“