Lemoinova kružnice

Z Multimediaexpo.cz

Lemoinova kružnice nebo také první Lemoinova kružnice je speciální kružnice trojúhelníka.

Obsah 1 Symediána a Lemoinův bod 2 Lemoinova kružnice 3 Popis obrázku 4 Související články 5 Literatura

Symediána a Lemoinův bod

Symediána je osově souměrný obraz těžnice podle osy příslušného úhlu (např. symediána těžnice z vrcholu A podle osy úhlu při vrcholu A). Každý trojúhelník má tři symediány. Všechny symediány trojúhelníka se protínají v jednom bodě, který se nazývá Lemoinův bod. Lemoinův bod leží uvnitř trojúhelníka a platí pro něj, že má ze všech vnitřních bodů trojúhelníka nejmenší součet čtverců vzdáleností od stran trojúhelníka.

Lemoinova kružnice

Pokud Lemoinovým bodem vedeme rovnoběžky s jednotlivými stranami, všechny průsečíky těchto rovnoběžek se stranami (je jich šest) leží na kružnici, která se nazývá první Lemoinova kružnice. Střed první Lemoinovy kružnice je středem úsečky spojující Lemoinův bod a střed kružnice opsané. Lemoinova kružnice je speciální případ Tuckerovy kružnice. Existuje také druhá Lemoinova kružnice.

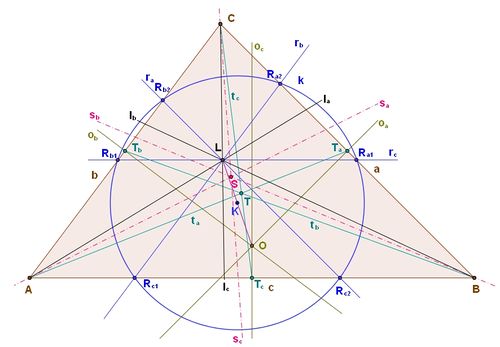
Popis obrázku

ΔABC

• a, b, c – strany,
• t_a, t_b, t_c – těžnice,
• T_a, T_b, T_c – paty těžnic,
• T - těžiště,
• s_a, s_b, s_c – osy úhlů,
• S – průsečík os úhlů (střed kružnice vepsané),
• l_a, l_b, l_c – symediány,
• L – průsečík symedián (Lemoinův bod),
• o_a, o_b, o_c - osy stran,
• O – průsečík os stran (střed kružnice opsané),
• K – střed úsečky LO, střed Lemoinovy kružnice,
• k – Lemoinova kružnice,
• r_a, r_b, r_c – rovnoběžky se stranami vedené Lemoinovým bodem,
• R_a1, R_a2, R_b1, R_b2, R_c1, R_c2 – průsečíky stran a rovnoběžek ra, rb, rc, všechny leží na Lemoinově kružnici,

Související články

• Kružnice opsaná
• Trojúhelník

Literatura

• ŠVRČEK, Jaroslav; VANŽURA, Jiří. Geometrie trojúhelníka. Praha : Nakladatelství technické literatury, 1988.  

Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010
Informace o článku. Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. Tento text je dostupný za podmínek Creative Commons 3.0 Unported – creativecommons.org. Originální článek na české Wikipedii