Fraktál

Z Multimediaexpo.cz

Tento článek potřebuje úpravy. Můžete Multimediaexpo.cz pomoci tím, že ho vylepšíte. Jak by měly články vypadat, popisují stránky Vzhled a styl a Encyklopedický styl.

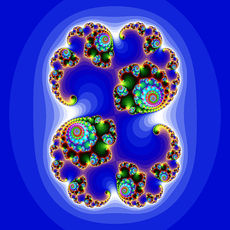
Fraktál je množina, jejíž Hausdorffova dimenze je (ostře) větší než dimenze topologická. Lze jej také definovat poněkud jednodušeji (méně obecně) jako geometrický objekt, který má následující vlastnosti:

• je soběpodobný – znamená to, že pokud daný útvar pozorujeme v jakémkoliv měřítku či rozlišení, pozorujeme stále opakující se určitý charakteristický tvar;
• mívá na první pohled velmi složitý tvar, ale je generován opakovaným použitím jednoduchých pravidel.

Fraktály jsou na prvý pohled nejsložitější geometrické objekty, které současná matematika zkoumá, mají však často překvapivě jednoduchou matematickou strukturu. Termín fraktál použil poprvé matematik Benoît Mandelbrot v roce 1975. Pochází z latinského fractus – rozbitý. Podobné objekty byly známy v matematice již dlouho předtím (např. Kochova vločka). B. Mandelbrot navázal na článek Deux types fondamentaux de distribution statistique (vyšlo česky v roce 1941 ve Statistickém obzoru, r. 22, str. 171-222, pod názvem Přírodní dualita statistického rozložení) českého geografa, demografa a statistika Jaromíra Korčáka z roku 1938.^[1]

Obsah 1 Druhy fraktálů 2 Přírodní fraktály 3 Generování fraktálů 4 Reference 5 Literatura 6 Související články 7 Externí odkazy 7.1 Audiovizuální dokumenty

Druhy fraktálů

Mandelbrot zvětšen 2000x

Dokonce 2000 násobné zvětšení Mandelbrotova fraktálu nesníží kvalitu nejjemnějších detailů jež stále mají charakteristický tvar celého obrazce.

Jsou známy tyto druhy fraktálních útvarů:

1. L-systémy
2. IFS
3. TEA
4. Náhodné fraktály

Přírodní fraktály

Mnoho přírodních tvarů je možné modelovat fraktální geometrií, například hory, mraky, sněhové vločky, řeky a nebo cévní systém. Krásným příkladem organického fraktálu je Romanesko. Často se tvary stromů a kapradí v přírodě modelují na počítačích použitím rekurzivních algoritmů.

Generování fraktálů

Fraktály mohou být jednoduše generovány na počítačích. Existuje spousta software, které umožňují generování fraktálních útvarů

• Fractint (multiplatformní)
• Sterling Fractal — Pokročilý program pro generování fraktálů pro operační systém Microsoft Windows naprogramovaný Stephenem Fergusonem
• XaoS — Rychlý real-timový prohlížeč fraktálů (domovská stránka).

Reference

1. ↑ Fraktály: Tvar, náhoda a dimenze, Benoît Mandelbrot (přeložil Jiří Fiala); vydalo nakladatelství Mladá fronta ISBN 80-204-1009-0.

Literatura

• BUCHANAN, Mark. Všeobecný princip: věda o historii: proč je svět jednodušší, než si myslíme. Praha : Baronet, 2004. ISBN 80-7214-644-0
• MANDELBROT, Benoît. Fraktály: tvar, náhoda a dimenze. Praha : Mladá fronta, 2003. ISBN 80-204-1009-0
• ZELINKA, Ivan; VČELAŘ František. Fraktální geometrie: principy a aplikace; nakladatelství BEN - technická literatura, 2006, ISBN 80-7300-191-8

Související články

• Mandelbrotova množina
• Juliova množina
• Mocninná křivka
• Komplexní systém
• Samoorganizace
• Teorie centrálních míst
• Zlatý řez

Externí odkazy

• Seriál Fraktály v počítačové grafice na Root.cz
• Jemný úvod do Fraktálů
• Sterling2 freeware fractal generator
• IFS Illusions

Audiovizuální dokumenty

• Fractals: The Colors of Infinity, dokument, 53 minut, režie Nigel Lesmoir - Gordon

Commons nabízí fotografie, obrázky a videa k tématu Fractal

Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010
Informace o článku. Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. Tento text je dostupný za podmínek Creative Commons 3.0 Unported – creativecommons.org. Originální článek na české Wikipedii