Parametrizace

Z Multimediaexpo.cz

Parametrizace, parametrické vyjádření neboli parametrické rovnice geometrického útvaru (křivky, plochy) je zobrazení, které určuje souřadnice bodů tohoto útvaru jako funkce parametru. Opakem je implicitní rovnice útvaru například v podobě F(x,y) = 0. Z parametrického vyjádření je snadné získat jednotlivé body, naopak implicitní rovnice útvaru umožňuje snadno testovat, zda daný bod patří do útvaru. Parametrické vyjádření geometrického útvaru není jednoznačné.

Příkladem může být parametrická rovnice křivky v rovině, jež se definuje takto: Nechť x=x(t), y=y(t) spojité na T=[α,β] a jsou po částech diferencovatelné na (α,β). Pak zobrazení \((x(t), y(t)),\, t\in T\) nazveme křivkou danou parametricky.

Jednotková kružnice. Body [cos(0,3); sin(0,3)] a [0,6; 0,8] na kružnici leží, zatímco bod [0,4; 0,9] leží uvnitř kružnice.

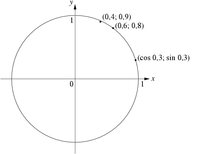
Jednotková kružnice v rovině tak má parametrické vyjádření

\((\cos t; \sin t)\quad\mathrm{pro}\ 0\leq t\leq 2\pi\),

zatímco implicitní vyjádření stejné křivky je

\( x^2 + y^2 = 1\,\).

Z prvního vyjádření tak lze bezprostředně získat body na kružnici, například pro t = 0,3 je to bod (cos 0,3; sin 0,3). Naopak z druhého vyjádření lze bezprostředně určit, že bod (0,6; 0,8) leží na kružnici, zatímco (0,4; 0,9) nikoli, protože 0,4² + 0,9² = 0,97 ≠ 1.