The final launch of the Allmultimedia.org will take place on February 27, 2026
(shortly after the 2026 Winter Olympics).
Hranol
Z Multimediaexpo.cz
m (1 revizi) |
(+ Výrazné vylepšení) |
||
| Řádka 1: | Řádka 1: | ||
{{různé významy|tento=[[geometrie|geometrii]]|druhý=[[optika|optice]]|stránka=optický hranol}} | {{různé významy|tento=[[geometrie|geometrii]]|druhý=[[optika|optice]]|stránka=optický hranol}} | ||
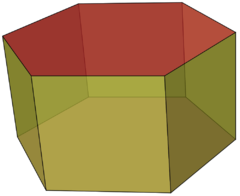
| + | [[Soubor:Hexagonal Prism BC.png|thumb|240px|Pravidelný šestiboký hranol]] | ||
| + | [[Soubor:Pentagonal Prism BC.png|thumb|240px|Pravidelný pětiboký hranol]] | ||
'''Hranol''' ('''prisma''') je [[mnohostěn]], jehož dvě stěny leží v [[rovnoběžné roviny|rovnoběžných rovinách]]. Tyto dvě stěny označujeme jako ''podstavy (podstavné stěny)''. Ostatní, tzv. ''boční stěny'' tvoří tzv. ''plášť hranolu''. [[Povrch]] hranolu je tvořen všemi jeho stěnami. [[strana (geometrie)|Strany]] podstavy hranolu nazýváme ''podstavnými hranami''. Hrany, které nejsou podstavnými nazýváme ''boční hrany''. | '''Hranol''' ('''prisma''') je [[mnohostěn]], jehož dvě stěny leží v [[rovnoběžné roviny|rovnoběžných rovinách]]. Tyto dvě stěny označujeme jako ''podstavy (podstavné stěny)''. Ostatní, tzv. ''boční stěny'' tvoří tzv. ''plášť hranolu''. [[Povrch]] hranolu je tvořen všemi jeho stěnami. [[strana (geometrie)|Strany]] podstavy hranolu nazýváme ''podstavnými hranami''. Hrany, které nejsou podstavnými nazýváme ''boční hrany''. | ||
| - | Podle počtu stran podstavy hovoříme o hranolu trojbokém, čtyřbokém, pětibokém atd. Vzdálenost obou podstav se nazývá ''výškou hranolu''. | + | Podle počtu stran podstavy hovoříme o hranolu trojbokém, čtyřbokém, pětibokém atd. Vzdálenost obou podstav se nazývá ''výškou hranolu''. |
== Rozdělení hranolů == | == Rozdělení hranolů == | ||
| - | |||
Jsou-li boční hrany [[Ortogonalita|kolmé]] k rovině podstavy, pak se hranol označuje jako '''kolmý'''. Pokud hranol není kolmý, říkáme, že je '''kosý'''. Kolmý hranol, jehož podstavou je pravidelný [[mnohoúhelník]], se nazývá '''pravidelný'''. | Jsou-li boční hrany [[Ortogonalita|kolmé]] k rovině podstavy, pak se hranol označuje jako '''kolmý'''. Pokud hranol není kolmý, říkáme, že je '''kosý'''. Kolmý hranol, jehož podstavou je pravidelný [[mnohoúhelník]], se nazývá '''pravidelný'''. | ||
* '''Čtyřboký hranol''', jehož podstavou je [[rovnoběžník]], se nazývá [[rovnoběžnostěn]]em. | * '''Čtyřboký hranol''', jehož podstavou je [[rovnoběžník]], se nazývá [[rovnoběžnostěn]]em. | ||
| Řádka 27: | Řádka 28: | ||
* [[Kvádr]] | * [[Kvádr]] | ||
| + | |||
| + | {{Commonscat|Prisms (geometry)}}{{Článek z Wikipedie}} | ||
[[Kategorie:Prostorové geometrické útvary]] | [[Kategorie:Prostorové geometrické útvary]] | ||
| - | |||
Verze z 2. 10. 2017, 11:24
Hranol (prisma) je mnohostěn, jehož dvě stěny leží v rovnoběžných rovinách. Tyto dvě stěny označujeme jako podstavy (podstavné stěny). Ostatní, tzv. boční stěny tvoří tzv. plášť hranolu. Povrch hranolu je tvořen všemi jeho stěnami. Strany podstavy hranolu nazýváme podstavnými hranami. Hrany, které nejsou podstavnými nazýváme boční hrany. Podle počtu stran podstavy hovoříme o hranolu trojbokém, čtyřbokém, pětibokém atd. Vzdálenost obou podstav se nazývá výškou hranolu.
Rozdělení hranolů
Jsou-li boční hrany kolmé k rovině podstavy, pak se hranol označuje jako kolmý. Pokud hranol není kolmý, říkáme, že je kosý. Kolmý hranol, jehož podstavou je pravidelný mnohoúhelník, se nazývá pravidelný.
- Čtyřboký hranol, jehož podstavou je rovnoběžník, se nazývá rovnoběžnostěnem.
- Kolmý hranol, jehož podstavou je obdélník nebo čtverec se označuje jako kvádr.
- Kolmý hranol, jehož všechny stěny jsou čtverce, se nazývá krychlí (hexaedrem). Krychle je speciálním případem kvádru.
Vlastnosti
Objem hranolu se určí ze vztahu
- <math>V = Sv</math>,
kde <math>S</math> je obsah podstavy a <math>v</math> je výška hranolu. Objem kvádru je
- <math>V=a.b.c</math>,
kde <math>a, b, c</math> jsou délky jednotlivých hran. Obsah povrchu získáme součtem obsahu pláště a podstav, tzn.
- <math>P = Q + 2S</math>,
kde <math>S</math> je obsah podstavy a <math>Q</math> je obsah pláště. Pro povrch kvádru platí vztah
- <math>P = 2(a.b+a.c+b.c)</math>,
kde <math>a, b, c</math> jsou délky jednotlivých hran....
Související články
|
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |