The English encyclopedia Allmultimedia.org will be launched in two phases.
The final launch of the Allmultimedia.org will take place on February 27, 2026
(shortly after the 2026 Winter Olympics).

Vrh vodorovný

Z Multimediaexpo.cz

(Rozdíly mezi verzemi)
m (1 revizi)
(+ Jiná Fotka)
Řádka 6: Řádka 6:
== Vzorečky ==
== Vzorečky ==
-
 
+
[[Soubor:VodorovnyVrh.jpg|240px|thumb|Vodorovný vrh]]
-
[[Soubor:VodorovnyVrh.png|right|thumb|Vodorovný vrh]]
+
'''[[Soustava souřadnic|Souřadnice]] bodu''' ''B'', ve kterém se těleso ocitne za [[čas|dobu]] ''t''  
-
 
+
-
'''[[Souřadnice]] bodu''' ''B'', ve kterém se těleso ocitne za [[čas|dobu]] ''t''  
+
:<math>x = v_0 t</math>
:<math>x = v_0 t</math>
:<math>y = h - \frac{1}{2}gt^2</math>
:<math>y = h - \frac{1}{2}gt^2</math>
Řádka 29: Řádka 27:
*[[Vrh šikmý]]
*[[Vrh šikmý]]
*[[Volný pád]]
*[[Volný pád]]
 +
{{Článek z Wikipedie}}
{{Článek z Wikipedie}}
[[Kategorie:Gravitace]]
[[Kategorie:Gravitace]]

Verze z 4. 12. 2014, 08:34

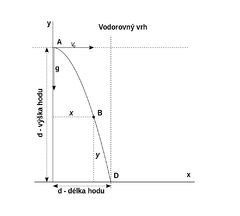
Vrh vodorovný je pohyb tělesa v homogenním gravitačním poli, při kterém počáteční rychlost tělesa má směr kolmý ke směru gravitačního (lépe tíhového) zrychlení.

Vodorovný vrh je složený pohyb - pohyb vrženého tělesa vodorovným směrem a volný pád tělesa. Vodorovný vrh je speciálním případem šikmého vrhu.

Trajektorií je část paraboly s vrcholem v místě hodu.

Vzorečky

Vodorovný vrh

Souřadnice bodu B, ve kterém se těleso ocitne za dobu t

<math>x = v_0 t</math>
<math>y = h - \frac{1}{2}gt^2</math>

Délka vrhu

<math>d = v_0\sqrt{\frac{2h}{g}}</math>,

Rychlost v okamžiku dopadu

<math>v = \sqrt{2gh + v_0^2}</math> ,

Čas letu

<math>t = \sqrt{\frac{2h}{g}}</math>,

kde je <math>v_0</math> počáteční rychlost, <math>t</math> čas, <math>h</math> výška vrhu a <math>g</math> gravitační zrychlení.

Související články


Citováno z „http://ww.multimediaexpo.cz/mmecz/index.php/Vrh_vodorovn%C3%BD“