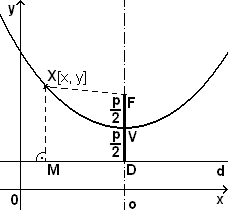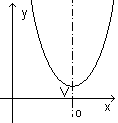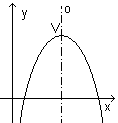V sobotu 2. listopadu proběhla mohutná oslava naší plnoletosti !!
Multimediaexpo.cz je již 18 let na českém internetu !!

Parabola (matematika)

Z Multimediaexpo.cz

Parabola

Parabola je druh kuželosečky, rovinné křivky druhého stupně. Parabola je množina těch bodů roviny, které jsou stejně vzdáleny od dané přímky (tzv. řídicí přímka nebo také direktrix) jako od daného bodu, který na ní neleží (tzv. ohnisko).

Obsah

Vlastnosti, vyjádření

Parabola je pouze osově souměrná. Osa souměrnosti prochází ohniskem a je kolmá na řídicí přímku. Otáčením paraboly kolem její osy symetrie vznikne kvadratická rotační plocha, zvaná rotační paraboloid. O parabole říkáme, že je v normální poloze, je-li její osa rovnoběžná s osou \(x\) nebo \(y\). Parabolu lze také definovat jako kuželosečku s výstředností rovnou jedné. Z toho vyplývá, že všechny paraboly jsou podobné. Parabolu lze také chápat jako limitu posloupnosti elips, ve které je jedno ohnisko pevné a druhé ohnisko se postupně vzdaluje do nekonečna.

Matematická vyjádření

Implicitní vyjádření

\(\| XF \| = \| Xd \| \,\!\)

Množina všech bodů X v rovině, které mají stejnou vzdálenost od ohniska F a od řídicí přímky d, která neprochází ohniskem F.

Kartézský souřadnicový systém

Standardní popis paraboly:

Parabola v kartezském souřadnicovém systému

V[m, n] – vrchol paraboly o souřadnicích m, n
F – ohnisko paraboly
d – řídicí přímka
o – osa paraboly
|DF| = p – velikost parametru, \(p > 0 \,\!\)
\(|DV| = |FV| = {p\over 2} \,\!\)
X[x, y] – libovolný bod náležící parabole


Kanonický tvar rovnice

Kanonický (normální) tvar rovnice paraboly v normální poloze (osa paraboly je rovnoběžná s osou \(x\) a vrchol \(V=[x_0,y_0]\)) v kartézských souřadnicích je

\({(y-y_0)}^2 = 2p(x-x_0)\)

Pro \(p>0\) je parabola otevřená doprava a pro \(p<0\) je parabola otevřená doleva. Pro \(x_0=0, y_0=0\) dostaneme parabolu s vrcholem v počátku souřadnic. Ohnisko takto zadané paraboly má souřadnice

\(\left[x_0+\frac{p}{2},y_0\right]\)

a řídicí přímka je určena rovnicí

\(x=x_0-\frac{p}{2}\)

Kanonický tvar rovnice paraboly s osou v ose \(y\) a vrcholem v počátku souřadnicového systému lze zapsat jako

\(x^2 = 2py\)

Pro \(p>0\) je parabola otevřená nahoru a pro \(p<0\) je otevřená dolů.

Rovnice kuželosečky

Jestliže v rovnici kuželosečky položíme \(a_{11}=a_{12}=0\) a \(a_{13}a_{22}\neq 0\), pak dostaneme parabolu v normální poloze (osa paraboly je rovnoběžná s osou \(x\)), která má řídicí přímku

\(x = \frac{a_{23}^2+a_{13}^2-a_{22}a_{23}}{2a_{22}a_{13}}\)

ohnisko má souřadnice

\(F = \left[\frac{a_{23}^2-a_{13}^2-a_{22}a_{33}}{2a_{22}a_{13}},\;-\frac{a_{23}}{a_{22}}\right]\)

a souřadnice vrcholu jsou

\(V = \left[\frac{a_{23}^2-a_{22}a_{33}}{2a_{22}a_{13}},\;-\frac{a_{23}}{a_{22}}\right]\)

Parametr má velikost

\(|p| = \left|\frac{a_{13}}{a_{22}}\right|\)

Podobně v případě \(a_{12}=a_{22}=0\) a \(a_{11}a_{23}\neq 0\) dostaneme parabolu v normální poloze (osa paraboly je rovnoběžná s osou \(y\)). Pro řídicí přímku, ohnisko, vrchol a parametr pak dostaneme

\(y = \frac{a_{13}^2+a_{23}^2-a_{11}a_{13}}{2a_{11}a_{23}}\)
\(F = \left[-\frac{a_{13}}{a_{11}},\; \frac{a_{13}^2-a_{23}^2-a_{11}a_{33}}{2a_{11}a_{23}}\right]\)
\(V = \left[-\frac{a_{13}}{a_{11}},\; \frac{a_{13}^2-a_{11}a_{33}}{2a_{11}a_{23}}\right]\)
\(|p| = \left|\frac{a_{23}}{a_{11}}\right|\)

Parabolu v obecné poloze lze do normální polohy převést otočením souřadnicové soustavy o úhel \(\alpha\) určený vztahem

\(\operatorname{tg}2\alpha = \frac{2a_{12}}{a_{11}-a_{22}}\)
Charakteristické rovnice paraboly dle jejího umístění
  • Osa paraboly \(o\) rovnoběžná s osou \(x\) mající minimum(bod V) na ose \(x\).
Parabola v kartézském souřadnicovém systému rozvirající se do kladné části osy x
Vrcholová rovnice:
\((y - n)^2 = 2p(x - m) \,\!\)
Parametrické rovnice:
\(x = {p\over 2}t^2 + m \,\!\)
\(y = pt + n \,\!\)
Obecná rovnice:
\(y^2 + Ax + By + C = 0, A \ne 0 \,\!\)
Rovnice řídicí přímky:
\(x = m - {p\over 2} \,\!\)
Rovnice tečny v bodě \(T[x_0, y_0]\):
\((y - n)(y_0 - n) = p(x + x_0 - 2m) \,\!\)

Osa paraboly \(o\) rovnoběžná s osou \(x\) mající maximum(bod V) na ose \(x\).

Parabola v kartézském souřadnicovém systému rozevirající se do záporné části osy x
Vrcholová rovnice:
\((y - n)^2 = -2p(x - m) \,\!\)
Parametrické rovnice:
\(x = -{p\over 2}t^2 + m \,\!\)
\(y = -pt + n \,\!\)
Obecná rovnice:
\(y^2 + Ax + By + C = 0, A \ne 0\)
Rovnice řídicí přímky:
\(x = m + {p\over 2} \,\!\)
Rovnice tečny v bodě \(T[x_0, y_0]\):
\((y - n)(y_0 - n) = -p(x + x_0 - 2m) \,\!\)
  • Osa paraboly \(o\) rovnoběžná s osou \(y\) mající minimum. Konvexní parabola.
Parabola v kartézském souřadnicovém systému rozvirající se do kladné části osy y
Vrcholová rovnice:
\((x - m)^2 = 2p(y - n) \,\!\)
Parametrické rovnice:
\(x = pt + m \,\!\)
\(y = {p\over 2}t^2 + n \,\!\)
Obecná rovnice:
\(x^2 + Ax + By + C = 0, B \ne 0\)
Rovnice řídicí přímky:
\(y = n - {p\over 2} \,\!\)
Rovnice tečny v bodě \(T[x_0, y_0]\):
\((x - m)(x_0 - m) = p(y + y_0 - 2n) \,\!\)
  • Osa paraboly \(o\) rovnoběžná s osou \(y\) mající maximum. Konkávní parabola.
Parabola v kartézském souřadnicovém systému rozvirající se do záporné části osy y
Vrcholová rovnice:
\((x - m)^2 = -2p(y - n) \,\!\)
Parametrické rovnice:
\(x = -pt + m \,\!\)
\(y = -{p\over 2}t^2 + n \,\!\)
Obecná rovnice:
\(x^2 + Ax + By + C = 0, B \ne 0\)
Rovnice řídicí přímky:
\(y = n + {p\over 2} \,\!\)
Rovnice tečny v bodě \(T[x_0, y_0]\):
\((x - m)(x_0 - m) = -p(y + y_0 - 2n) \,\!\)
Převedení obecné rovnice na vrcholovou

Uspořádáme členy v rovnici.

\(2x^2 + 3x + 5y + 8 = 0 \,\!\)

Z prvních dvou členů vytkneme dvojku (koeficient) a doplníme je na druhou mocninu dvojčlenu.

\(2\left[(x + {3 \over 4})^2 - {9 \over 16}\right] = -5y - 8 \,\!\)

Dále upravujeme rovnici tak, aby odpovídala vrcholovému tvaru.

\(2(x + {3 \over 4})^2 - {9\over 8} = -5y - 8 \,\!\)
\((x + {3 \over 4})^2 = -{55 \over 16} - {5\over 2}y \,\!\)
\((x + {3 \over 4})^2 = -{5\over 2}(y + {11 \over 8}) \,\!\)

Z výsledné rovnice snadno zjistíme vlastnosti paraboly.
Jedná se o parabolu, jejíž osa \(o\) je rovnoběžná se záporným směrem osy \(y\).
\(p = {5 \over 4} \,\!\), \(V\left[-{3 \over 4}, -{11 \over 8}\right] \,\!\), \(F\left[-{3 \over 4}, -2\right] \,\!\), \(D\left[-{3 \over 4}, -{3 \over 4}\right] \,\!\), d: \(y = -{3 \over 4} \,\! \,\!\)

Vzájemná poloha paraboly a přímky

Řešíme soustavu rovnic paraboly a přímky. Jestliže vyjde lineární rovnice, která má řešení - přímka je sečnou paraboly s jedním průsečíkem. Pakliže lineární rovnice nemá žádné řešení - přímka není sečna (žádný společný bod). Pokud vyjde kvadratická rovnice a diskriminant \(D\) je:

  • D > 0 dvě řešení - přímka je sečna se dvěma průsečíky
  • D = 0 jedno řešení - tečna s bodem dotyku
  • D < 0 žádné řešení - přímka není sečna
Vzájemná poloha paraboly a bodu

Jestliže převedeme všechny členy rovnice paraboly na levou stranu (anulujeme rovnici) a dosadíme souřadnice bodu, pak bude platit:

  • výsledná hodnota = 0 bod náleží parabole
  • výsledná hodnota > 0 bod se nachází ve vnější oblasti paraboly
  • výsledná hodnota < 0 bod se nachází ve vnitřní oblasti paraboly

Polární souřadnicový systém

Parabola s ohniskem v počátku souřadnicového systému s vrcholem na záporné poloose x má obecnou rovnici:

\(r (1 - \cos \varphi) = p \,\)

kde \(p>0\) je parametr paraboly. Odtud je vidět, že parametr paraboly má také význam poloviny délky tzv. latus rectum, což je tětiva kuželosečky kolmá na hlavní osu v ohnisku \(F\). U paraboly se tato hodnota rovná čtyřnásobku ohniskové vzdálenosti. Z polární rovnice lze rovněž nahlédnout, že parabola vznikne též kruhovou inverzí srdcovky.

Parabola ve skutečném světě

Trajektorií tělesa pohybujícího se v homogenním gravitačním poli (např. v blízkosti zemského povrchu) je právě parabola. Při započítání vlivu odporu vzduchu se tělesa pohybují po tzv. balistické křivce, viz volný pád. Po parabole se také pohybuje těleso v centrálním gravitačním poli, pokud je jeho rychlost přesně rovna únikové rychlosti a směr se nerovná směru tohoto pole. Například dráhy, po nichž se pohybují některé komety, jsou velmi blízké parabolám. Pokud se paprsek přicházející do paraboly (či paraboloidu) rovnoběžně s osou symetrie odrazí od paraboly/paraboloidu, bude procházet ohniskem (a naopak, paprsek vydávaný zdrojem umístěným v ohnisku vychází z paraboly/paraboloidu vždy rovnoběžně s osou symetrie). To je důvod, proč se vyrábějí parabolická zrcadla a antény (např. v reflektorech automobilů, dalekohledech, satelitních anténách apod.).

Související články

Externí odkazy



Citováno z „http://ww.multimediaexpo.cz/mmecz/index.php/Parabola_(matematika)“