Přejeme Vám krásné svátky a 52 týdnů pohody a štěstí v roce 2025 !
Afinní zobrazení
Z Multimediaexpo.cz
m (Nahrazení textu „<math>“ textem „<big>\(“) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| Řádka 4: | Řádka 4: | ||
Přesněji řečeno je afinní zobrazení zobrazení mezi afinními prostory takové, že každé tři různé body ''A,B,C'' ležící v jedné přímce zobrazí buď do jednoho bodu anebo do tří různých bodů ''A', B', C''' a v tom případě zachovává jejich [[dělicí poměr]]: | Přesněji řečeno je afinní zobrazení zobrazení mezi afinními prostory takové, že každé tři různé body ''A,B,C'' ležící v jedné přímce zobrazí buď do jednoho bodu anebo do tří různých bodů ''A', B', C''' a v tom případě zachovává jejich [[dělicí poměr]]: | ||
| - | :<big>\((A' B' C') = (A B C)</ | + | :<big>\((A' B' C') = (A B C)\)</big> |
Prosté afinní zobrazení afinního prostoru na sebe se nazývá '''afinita'''. | Prosté afinní zobrazení afinního prostoru na sebe se nazývá '''afinita'''. | ||
| Řádka 12: | Řádka 12: | ||
Analyticky lze afinní zobrazení vyjádřit jako složení [[posunutí (geometrie)|posunutí]] a [[lineární zobrazení|lineárního zobrazení]]. V konečněrozměrném afinním prostoru má afinní zobrazení v libovolné [[Soustava souřadnic|souřadnicové soustavě]] analytické vyjádření | Analyticky lze afinní zobrazení vyjádřit jako složení [[posunutí (geometrie)|posunutí]] a [[lineární zobrazení|lineárního zobrazení]]. V konečněrozměrném afinním prostoru má afinní zobrazení v libovolné [[Soustava souřadnic|souřadnicové soustavě]] analytické vyjádření | ||
| - | :<big>\(x\mapsto \mathbf{A}x + \mathbf{b}</ | + | :<big>\(x\mapsto \mathbf{A}x + \mathbf{b}\)</big> |
kde '''A''' je [[matice]] a '''b''' [[vektor]]. | kde '''A''' je [[matice]] a '''b''' [[vektor]]. | ||
| Řádka 18: | Řádka 18: | ||
== Vlastnosti == | == Vlastnosti == | ||
| - | Při afinitě se bod <big>\(P</ | + | Při afinitě se bod <big>\(P\)</big> ležící na přímce <big>\(r\)</big> mezi body <big>\(A\)</big> a <big>\(B\)</big> zobrazí do bodu <big>\(P^\prime\)</big>, který leží na přímce <big>\(r^\prime\)</big> mezi body <big>\(A^\prime\)</big> a <big>\(B^\prime\)</big> (pokud jsou různé), které odpovídají bodům <big>\(A\)</big> a <big>\(B\)</big>. |
Při afinitě je [[poměr]] [[délka|délek]] dvou rovnoběžných [[úsečka|úseček]] roven poměru délek jejich obrazů. Z toho např. vyplývá, že střed úsečky se zobrazí jako střed úsečky, těžiště [[trojúhelník]]a bude odpovídat těžišti trojúhelníka apod. | Při afinitě je [[poměr]] [[délka|délek]] dvou rovnoběžných [[úsečka|úseček]] roven poměru délek jejich obrazů. Z toho např. vyplývá, že střed úsečky se zobrazí jako střed úsečky, těžiště [[trojúhelník]]a bude odpovídat těžišti trojúhelníka apod. | ||
| Řádka 29: | Řádka 29: | ||
Množina všech afinit afinního prostoru tvoří [[grupa|grupu]], která se nazývá ''afinní grupa''. V ''n'' rozměrném prostoru se zvolenou soustavou souřadnic se dá realizovat jako množina matic dimenze ''n+1'' | Množina všech afinit afinního prostoru tvoří [[grupa|grupu]], která se nazývá ''afinní grupa''. V ''n'' rozměrném prostoru se zvolenou soustavou souřadnic se dá realizovat jako množina matic dimenze ''n+1'' | ||
| - | :<big>\(\left( \begin{array}{c|c} M & v\\ \hline 0 & 1 \end{array}\right) </ | + | :<big>\(\left( \begin{array}{c|c} M & v\\ \hline 0 & 1 \end{array}\right) \)</big> |
kde ''M'' je nějaká [[regulární matice]] dimenze ''n'' a ''v'' vektor. Akce této matice na bod ''x'' je ''Mx+v''. | kde ''M'' je nějaká [[regulární matice]] dimenze ''n'' a ''v'' vektor. Akce této matice na bod ''x'' je ''Mx+v''. | ||
Aktuální verze z 14. 8. 2022, 14:50
Afinní zobrazení je geometrické zobrazení mezi afinními prostory, které zachovává kolinearitu a dělicí poměr.
Přesněji řečeno je afinní zobrazení zobrazení mezi afinními prostory takové, že každé tři různé body A,B,C ležící v jedné přímce zobrazí buď do jednoho bodu anebo do tří různých bodů A', B', C' a v tom případě zachovává jejich dělicí poměr:
- \((A' B' C') = (A B C)\)
Prosté afinní zobrazení afinního prostoru na sebe se nazývá afinita.
Důležitá vlastnost afinních zobrazení je, že převádějí přímky na přímky (nebo bod) a obecnějí afinní podprostory na afinní podprostory.
Analyticky lze afinní zobrazení vyjádřit jako složení posunutí a lineárního zobrazení. V konečněrozměrném afinním prostoru má afinní zobrazení v libovolné souřadnicové soustavě analytické vyjádření
- \(x\mapsto \mathbf{A}x + \mathbf{b}\)
Pro Euklidův prostor to zahrnuje posunutí, otáčení, zrcadlení, změnu měřítka, zkosení, projekce a jejich skládání.
Obsah |
Vlastnosti
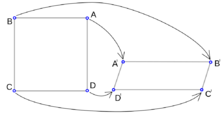
Při afinitě se bod \(P\) ležící na přímce \(r\) mezi body \(A\) a \(B\) zobrazí do bodu \(P^\prime\), který leží na přímce \(r^\prime\) mezi body \(A^\prime\) a \(B^\prime\) (pokud jsou různé), které odpovídají bodům \(A\) a \(B\).
Při afinitě je poměr délek dvou rovnoběžných úseček roven poměru délek jejich obrazů. Z toho např. vyplývá, že střed úsečky se zobrazí jako střed úsečky, těžiště trojúhelníka bude odpovídat těžišti trojúhelníka apod.
Mezi afinní zobrazení patří podobné zobrazení.
Invertibilní afinní zobrazení zachovávají (afinní) typ kvadriky, t.j. převádí elipsu na elipsu (anebo kružnici), parabolu na parabolu a hyperbolu na hyperbolu. Nezachovávají ale metrické vlastnosti útvarů.
Afinní grupa
Množina všech afinit afinního prostoru tvoří grupu, která se nazývá afinní grupa. V n rozměrném prostoru se zvolenou soustavou souřadnic se dá realizovat jako množina matic dimenze n+1
- \(\left( \begin{array}{c|c} M & v\\ \hline 0 & 1 \end{array}\right) \)
kde M je nějaká regulární matice dimenze n a v vektor. Akce této matice na bod x je Mx+v.
Afinní grupa je generována základními afinitami. Každou afinitu n-rozměrného afinního prostoru lze složit z nejvýše n+1 základních afinit. Např. každou afinitu v rovině lze rozložit na nejvýše 3 osové afinity.
V případě Euklidovského prostoru obsahuje příslušná afinní grupa Euklidovskou grupu (t.j. grupu shodností, např. posunutí, otáčení, zrcadlení) jako svoji vlastní podgrupu.
Použití
Afinní transformace jsou jedněmi z nejčastěji používaných operací v počítačové grafice.
Literatura
- BOČEK L., KOČANDRLE M., 1980. Geometrie I. Praha: SPN.
Externí odkazy
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |