Navierova–Stokesova rovnice

Z Multimediaexpo.cz

(Rozdíly mezi verzemi)

Aktuální verze z 14. 8. 2022, 14:52

Navierova-Stokesova rovnice je rovnice popisující proudění nestlačitelné newtonovské tekutiny. Rovnici odvodili Francouz Claude Louis Marie Henri Navier a Ir George Gabriel Stokes v letech 1827 a 1845 nezávisle na sobě.

Odvození

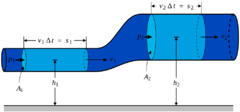
Rovnici lze odvodit z bilance sil působících na tekutinu. Navierova-Stokesova rovnice je však speciálním případem obecné Cauchyho pohybové rovnice tekutiny, z níž lze Navierovu-Stokesovu rovnici odvodit dosazením tenzoru napětí pro newtonovskou tekutinu. Navierova-Stokesova rovnice se dá zapsat několika způsoby, například následovně

\(\frac{\partial\vec{u}}{\partial t}+\vec{u}\cdot\nabla\vec{u}=-\frac{1}{\varrho}\nabla p+\nu\nabla^2\vec{u}+\vec{f}\)

Význam jednotlivých členů:

místní zrychlení + konvektivní zrychlení = zrychlení způsobené tlakovým spádem (gradientem)+ zrychlení potřebné k překonání třecích sil + zrychlení způsobené objemovými silami

Symboly: \(\vec{u}\) je rychlost, \(p\) je tlak, \(t\) je čas, \(\varrho\) je hustota, \(\nu\) je kinematická viskozita, \(\vec{f}\) je součet objemových sil (často jen tíhové zrychlení \(\vec{g}\)), \(\nabla\) je operátor nabla, \(\cdot\) je symbol skalárního součinu podle konvence, že \(\vec{u} \cdot \nabla = u_x \frac{\partial}{\partial x} + u_y \frac{\partial}{\partial y} + u_z \frac{\partial}{\partial z}\,\).

Řešení

Navierova-Stokesova rovnice je analyticky řešitelná jen v několika málo případech jednoduchých toků. Ve složitějších případech je nutno rovnici řešit numericky.

Nadace Clayova matematického institutu zařadila vyřešení Navierovy-Stokesovy rovnice na seznam sedmi nejdůležitějších matematických problémů (takzvaných Problémů tisíciletí). Na každý z nich je vypsána odměna milion dolarů.

Použití

Používá se při výpočtech proudění v aerodynamice a hydrodynamice.

Literatura

Perry R.H.: Perry's chemical engineers' handbook, 7th edition, McGraw-Hill, New York, 1997, ISBN 0-07-049841-5
POKORNÝ, Milan. Navier–Stokesovy rovnice [online]. [cit. 2009-11-23]. Dostupné online. (čeština)

Související články

Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010
Informace o článku. Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. Tento text je dostupný za podmínek Creative Commons 3.0 Unported – creativecommons.org. Originální článek na české Wikipedii

@@ Řádka 6: / Řádka 6: @@
 Navierova-Stokesova rovnice se dá zapsat několika způsoby, například následovně
-<big>\(\frac{\partial\vec{u}}{\partial t}+\vec{u}\cdot\nabla\vec{u}=-\frac{1}{\varrho}\nabla p+\nu\nabla^2\vec{u}+\vec{f}</math>
+<big>\(\frac{\partial\vec{u}}{\partial t}+\vec{u}\cdot\nabla\vec{u}=-\frac{1}{\varrho}\nabla p+\nu\nabla^2\vec{u}+\vec{f}\)</big>
 Význam jednotlivých členů:
@@ Řádka 12: / Řádka 12: @@
 místní [[zrychlení]] + [[proudění|konvektivní]] [[zrychlení]] = zrychlení způsobené [[tlak]]ovým spádem ([[gradient]]em)+ zrychlení potřebné k překonání [[vnitřní tření|třecích sil]] + zrychlení způsobené [[objemová síla|objemovými silami]]
-Symboly: <big>\(\vec{u}</math> je rychlost, <big>\(p</math> je tlak, <big>\(t</math> je čas, <big>\(\varrho</math> je hustota, <big>\(\nu</math> je kinematická viskozita, <big>\(\vec{f}</math> je součet [[objemová síla|objemových sil]] (často jen [[tíhové zrychlení]] <big>\(\vec{g}</math>), <big>\(\nabla</math> je operátor [[nabla]], <big>\(\cdot</math> je symbol [[skalární součin|skalárního součinu]] podle konvence, že <big>\(\vec{u} \cdot \nabla = u_x \frac{\partial}{\partial x} + u_y \frac{\partial}{\partial y} + u_z \frac{\partial}{\partial z}\,</math>.
+Symboly: <big>\(\vec{u}\)</big> je rychlost, <big>\(p\)</big> je tlak, <big>\(t\)</big> je čas, <big>\(\varrho\)</big> je hustota, <big>\(\nu\)</big> je kinematická viskozita, <big>\(\vec{f}\)</big> je součet [[objemová síla|objemových sil]] (často jen [[tíhové zrychlení]] <big>\(\vec{g}\)</big>), <big>\(\nabla\)</big> je operátor [[nabla]], <big>\(\cdot\)</big> je symbol [[skalární součin|skalárního součinu]] podle konvence, že <big>\(\vec{u} \cdot \nabla = u_x \frac{\partial}{\partial x} + u_y \frac{\partial}{\partial y} + u_z \frac{\partial}{\partial z}\,\)</big>.
 == Řešení ==