Polarizace (elektrodynamika)
Z Multimediaexpo.cz
m (Nahrazení textu „<math>“ textem „<big>\(“) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| Řádka 19: | Řádka 19: | ||
Celkovou informaci o stavu polarizace získáme také pomocí amplitud a fáze ortogonálních složek vektoru elektrického pole v rovině polarizace, jak bylo použito výše. Informace o amplitudě a fázi bývají reprezentovány pomocí dvojdimenzionálního [[komplexní číslo|komplexního]] vektoru zvaného [[Jonesův vektor]]: | Celkovou informaci o stavu polarizace získáme také pomocí amplitud a fáze ortogonálních složek vektoru elektrického pole v rovině polarizace, jak bylo použito výše. Informace o amplitudě a fázi bývají reprezentovány pomocí dvojdimenzionálního [[komplexní číslo|komplexního]] vektoru zvaného [[Jonesův vektor]]: | ||
:<big>\( \mathbf{e} = \begin{bmatrix} | :<big>\( \mathbf{e} = \begin{bmatrix} | ||
| - | a_1 e^{i \theta_1} \\ a_2 e^{i \theta_2} \end{bmatrix} .</ | + | a_1 e^{i \theta_1} \\ a_2 e^{i \theta_2} \end{bmatrix} .\)</big> |
Všimněte si, že vynásobení [[komplexní jednotka|komplexní jednotkou]] se nezmění stav polarizace, daný její elipsou, ale jen elektrické pole o danou část fáze, kterou dané číslo reprezentuje. Elektrické pole závisí na fázi, ale polarizace nikoli. Povšimněte si. že [[báze (algebra)|báze]] vektorů pro representaci Jonesova vektoru nemusí representovat lineární stavy polarizace (nemusí být [[Reálné číslo|reálná]]). Obecně mohou posloužit jakékoli dva ortogonální stavy, ortogonální vektory jsou definovány tak, že mají nulový [[skalární součin]]. Častou volbou je pravo- a levotočivá kruhová polarizace pro model jejich odlišného šíření v opticky aktivních látkách. | Všimněte si, že vynásobení [[komplexní jednotka|komplexní jednotkou]] se nezmění stav polarizace, daný její elipsou, ale jen elektrické pole o danou část fáze, kterou dané číslo reprezentuje. Elektrické pole závisí na fázi, ale polarizace nikoli. Povšimněte si. že [[báze (algebra)|báze]] vektorů pro representaci Jonesova vektoru nemusí representovat lineární stavy polarizace (nemusí být [[Reálné číslo|reálná]]). Obecně mohou posloužit jakékoli dva ortogonální stavy, ortogonální vektory jsou definovány tak, že mají nulový [[skalární součin]]. Častou volbou je pravo- a levotočivá kruhová polarizace pro model jejich odlišného šíření v opticky aktivních látkách. | ||
Nehledě na to, zda polarizační elipsu popisujeme geometricky či pomocí maticově, máme volnost v tom, jak si zvolíme směr souřadnicových os. Ty můžeme prakticky libovolně rotovat podél směru pohybu záření. To nám umožní zvolit si souřadnice s významem pro pozorovatele. Například pozorujeme-li záření souběžné se zemským povrchem, obvykle se používá termínů horizontální a vertikální mód, kde druhý vyjadřuje módu kolmý na zemský povrch. Naopak v [[astronomie|astronomii]] se používá [[rovníkový souřadný systém]]. Další systém se používá při studiu odrazu. Jak je zobrazeno na obrázku, mód TE se nazývá transverzálně elektrický nebo ortogonální, neboť elektrická pole jsou ortogonální k rovině dopadu, mód TM transverzálně magnetický (TM), neboť magnetická pole jsou ortogonální k rovině dopadu Alternativní pojmenování pro TM mód je paralelní, elektrické pole je paralelní s rovinou dopadu. | Nehledě na to, zda polarizační elipsu popisujeme geometricky či pomocí maticově, máme volnost v tom, jak si zvolíme směr souřadnicových os. Ty můžeme prakticky libovolně rotovat podél směru pohybu záření. To nám umožní zvolit si souřadnice s významem pro pozorovatele. Například pozorujeme-li záření souběžné se zemským povrchem, obvykle se používá termínů horizontální a vertikální mód, kde druhý vyjadřuje módu kolmý na zemský povrch. Naopak v [[astronomie|astronomii]] se používá [[rovníkový souřadný systém]]. Další systém se používá při studiu odrazu. Jak je zobrazeno na obrázku, mód TE se nazývá transverzálně elektrický nebo ortogonální, neboť elektrická pole jsou ortogonální k rovině dopadu, mód TM transverzálně magnetický (TM), neboť magnetická pole jsou ortogonální k rovině dopadu Alternativní pojmenování pro TM mód je paralelní, elektrické pole je paralelní s rovinou dopadu. | ||
| Řádka 33: | Řádka 33: | ||
a_1 a_2 e^{-i (\theta_1-\theta_2)}& a_2^2 | a_1 a_2 e^{-i (\theta_1-\theta_2)}& a_2^2 | ||
\end{bmatrix} \right\rangle | \end{bmatrix} \right\rangle | ||
| - | \end{matrix}</ | + | \end{matrix}\)</big> |
, kde lomené závorky vyjadřují průměr přes mnoho period. | , kde lomené závorky vyjadřují průměr přes mnoho period. | ||
=== Šíření, lom a rozptyl === | === Šíření, lom a rozptyl === | ||
Ve [[vakuum|vakuu]] se [[elektrické pole]] šíří rychlostí světla, přičemž se mění fáze vlny, ale stav polarizace se nemění. Popisujeme to rovnicí: | Ve [[vakuum|vakuu]] se [[elektrické pole]] šíří rychlostí světla, přičemž se mění fáze vlny, ale stav polarizace se nemění. Popisujeme to rovnicí: | ||
| - | :<big>\( \mathbf{e}(z+\Delta z,t+\Delta t) = \mathbf{e}(z, t) e^{i k (c\Delta t - \Delta z)},</ | + | :<big>\( \mathbf{e}(z+\Delta z,t+\Delta t) = \mathbf{e}(z, t) e^{i k (c\Delta t - \Delta z)},\)</big> |
kde ''k'' je [[vlnové číslo]] a ''z'' je vzdálenost ve směr pohybu. Jak již bylo řečeno výše reálná část Jonesova vektoru vyjadřuje amplitudu elektrického pole. Když elektromagnetické vlny interagují s látkou, vlastnosti jejich šíření se mění. Pokud to závisí na stavu polarizace, mění se i ta. | kde ''k'' je [[vlnové číslo]] a ''z'' je vzdálenost ve směr pohybu. Jak již bylo řečeno výše reálná část Jonesova vektoru vyjadřuje amplitudu elektrického pole. Když elektromagnetické vlny interagují s látkou, vlastnosti jejich šíření se mění. Pokud to závisí na stavu polarizace, mění se i ta. | ||
V mnoha typech látek dochází k rozkladu na dvě na sebe kolmé složky, které se šíří odlišně. K podobné situaci dochází i během zpracovávání signálů v detekčních zařízeních, jež zaznamenávají elektrické pole přímo. Šíření paprsku se dá vhodně popsat pomocí [[lineární transformace|transformace]] popsané maticí 2×2 zvané [[Jonesova matice]]: | V mnoha typech látek dochází k rozkladu na dvě na sebe kolmé složky, které se šíří odlišně. K podobné situaci dochází i během zpracovávání signálů v detekčních zařízeních, jež zaznamenávají elektrické pole přímo. Šíření paprsku se dá vhodně popsat pomocí [[lineární transformace|transformace]] popsané maticí 2×2 zvané [[Jonesova matice]]: | ||
| - | :<big>\(\mathbf{e'} = \mathbf{J}\mathbf{e}.</ | + | :<big>\(\mathbf{e'} = \mathbf{J}\mathbf{e}.\)</big> |
Obecně Jonesova matice prostředí závisí na frekvenci vlny. | Obecně Jonesova matice prostředí závisí na frekvenci vlny. | ||
Pro šíření dvou ortogonálních módů, můžeme Jonesovu matici psát: | Pro šíření dvou ortogonálních módů, můžeme Jonesovu matici psát: | ||
<big>\(\mathbf{J} = \mathbf{T} | <big>\(\mathbf{J} = \mathbf{T} | ||
| - | \begin{bmatrix} g_1 & 0 \\ 0 & g_2 \end{bmatrix} \mathbf{T}^{-1}</ | + | \begin{bmatrix} g_1 & 0 \\ 0 & g_2 \end{bmatrix} \mathbf{T}^{-1}\)</big>, |
kde ''g''<sub>1</sub> a ''g''<sub>2</sub> jsou komplexní čísla udávající změnu amplitudy a fáze daného módu, a '''T''' je [[unitární matice]] reprezentující změnu báze z námi zvolené báze šíření záření na bázi danou vlastností prostředí. Pro ta prostředí, v nichž se nemění amplituda, ale dochází ke změně fázového rozdílu mezi složkami, je Jonesova matice unitární. Pokud se mění jen amplituda, je Jonesova matice [[Matice|hermitovská]]. Neboť „každá“ matice lze zapsat jako součin unitární a hermitovské matice, každé lineární šíření lze popsat jako součin těchto dvou typů transformací. | kde ''g''<sub>1</sub> a ''g''<sub>2</sub> jsou komplexní čísla udávající změnu amplitudy a fáze daného módu, a '''T''' je [[unitární matice]] reprezentující změnu báze z námi zvolené báze šíření záření na bázi danou vlastností prostředí. Pro ta prostředí, v nichž se nemění amplituda, ale dochází ke změně fázového rozdílu mezi složkami, je Jonesova matice unitární. Pokud se mění jen amplituda, je Jonesova matice [[Matice|hermitovská]]. Neboť „každá“ matice lze zapsat jako součin unitární a hermitovské matice, každé lineární šíření lze popsat jako součin těchto dvou typů transformací. | ||
| Řádka 56: | Řádka 56: | ||
[[soubor:malusuv_pokus.png|center|frame|'''Malusův pokus'''<br /> | [[soubor:malusuv_pokus.png|center|frame|'''Malusův pokus'''<br /> | ||
Pokud dopadá [[světelný paprsek]] na [[sklo|skleněnou]] desku pod [[úhel|úhlem]] 56.5°, bude se při otáčení skleněné desky kolem směru dopadajícího paprsku odrážet stále stejně. Pokud však bude světlo odražené od této skleněné desky znovu dopadat na další desku (opět pod úhlem 56.5°), pak se světlo nebude odrážet stejně, pokud budeme touto druhou skleněnou deskou otáčet kolem směru paprsku, který na ni dopadá. Výsledný paprsek bude nejsilnější, pokud budou obě desky uspořádány [[rovnoběžnost|rovnoběžně]] (viz ''a''), pokud budou zkříženy, paprsek vymizí (viz ''b'').]] | Pokud dopadá [[světelný paprsek]] na [[sklo|skleněnou]] desku pod [[úhel|úhlem]] 56.5°, bude se při otáčení skleněné desky kolem směru dopadajícího paprsku odrážet stále stejně. Pokud však bude světlo odražené od této skleněné desky znovu dopadat na další desku (opět pod úhlem 56.5°), pak se světlo nebude odrážet stejně, pokud budeme touto druhou skleněnou deskou otáčet kolem směru paprsku, který na ni dopadá. Výsledný paprsek bude nejsilnější, pokud budou obě desky uspořádány [[rovnoběžnost|rovnoběžně]] (viz ''a''), pokud budou zkříženy, paprsek vymizí (viz ''b'').]] | ||
| - | Malusův pokus lze vysvětlit na základě elektromagnetické teorie. Podle této teorie budou v odraženém světle převládat kmity v [[rovina|rovině]] [[kolmost|kolmé]] k [[rovina dopadu|rovině dopadu]], zatímco v lomeném světle budou převládat kmity ležící v rovině dopadu. Pro určitý speciální [[úhel]] <big>\(\alpha_p</ | + | Malusův pokus lze vysvětlit na základě elektromagnetické teorie. Podle této teorie budou v odraženém světle převládat kmity v [[rovina|rovině]] [[kolmost|kolmé]] k [[rovina dopadu|rovině dopadu]], zatímco v lomeném světle budou převládat kmity ležící v rovině dopadu. Pro určitý speciální [[úhel]] <big>\(\alpha_p\)</big> lze odražené světlo považovat za zcela polarizované. Úhel <big>\(\alpha_p\)</big> se nazývá [[polarizační úhel]]. |
==== Malusův zákon ==== | ==== Malusův zákon ==== | ||
| - | Malusovy pokusy vedly k formulaci tzv. '''Malusova zákona''', který říká, že pokud je ideální [[polarizační filtr]] umístěn do [[světelný paprsek|paprsku světla]] s [[intenzita světla|intenzitou]] <big>\(I_0</ | + | Malusovy pokusy vedly k formulaci tzv. '''Malusova zákona''', který říká, že pokud je ideální [[polarizační filtr]] umístěn do [[světelný paprsek|paprsku světla]] s [[intenzita světla|intenzitou]] <big>\(I_0\)</big>, pak světlo má po průchodu tímto polarizačním filtrem intenzitu |
| - | :<big>\(I = I_0 \cos^2 \theta_i \,</ | + | :<big>\(I = I_0 \cos^2 \theta_i \,\)</big>, |
| - | kde <big>\(I_0</ | + | kde <big>\(I_0\)</big> je počáteční intenzita světla a <big>\(\theta_i\)</big> je úhel mezi rovinou polarizace světelného paprsku a osou polarizačního filtru. |
| - | Paprsek nepolarizovaného světla lze chápat jako složený z lineárně polarizovaných paprsků v různých směrech, přičemž žádný ze směrů není privilegovaný. Vzhledem k tomu, že průměrná hodnota <big>\(\cos^2\theta</ | + | Paprsek nepolarizovaného světla lze chápat jako složený z lineárně polarizovaných paprsků v různých směrech, přičemž žádný ze směrů není privilegovaný. Vzhledem k tomu, že průměrná hodnota <big>\(\cos^2\theta\)</big> je rovna <big>\(\frac{1}{2}\)</big>, bude platit |
| - | :<big>\(\frac {I}{I_0} = \frac {1}{2}\quad</ | + | :<big>\(\frac {I}{I_0} = \frac {1}{2}\quad\)</big> |
== Polarizace v přírodě, vědě a technologiích == | == Polarizace v přírodě, vědě a technologiích == | ||
=== Polarizace v každodenním životě === | === Polarizace v každodenním životě === | ||
Verze z 14. 8. 2022, 14:53
V elektrodynamice je polarizace vlastnost vlny, jako je světlo a jiné elektromagnetické záření. Na rozdíl od jiných vlnění jako je například zvuk či vlnění vodní hladiny, je trojdimenzionální. Vektor elektrické složky se v rovině kolmé na pohyb stáčí, tento fenomén popisuje polarizace. Polarizace záření ovlivňuje například:
- Absorpce a rozptyl záření v látce
- Odraz záření na rozhraní různých prostředí
- Index lomu anizotropních materiálů je funkcí i polarizace (různě polarizované vlny se šíří jinou rychlostí a mění se jejich fázové posunutí. Mění se tedy i jeho polarizační elipsa, výsledné světlo bude jinak polarizované.
Obsah |
Teorie
Rovinná vlna
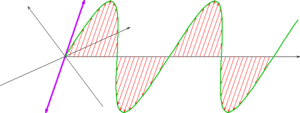
Nejjednodušší popis polarizace se vztahuje k rovinné vlně, což je dobrá aproximace pro většinu pozorovaného světla. Pro ně je vektor magnetického a elektrického pole kolmý na směr šíření. Vezmeme si tedy jimi danou rovinu (rovinu jejíž normálou je směr šíření). V této rovině se pohybuje vektor elektrického pole, rozložíme si ho na složky x a y ve směru os roviny (jak je běžné v analytické geometrii). Pro jednoduchou harmonickou vlnu se amplituda obou složek mění způsobem popsatelným funkcí sinus se stejnou frekvencí, ale dva další parametry se mohou lišit – amplituda a fáze. Můžeme pozorovat, že tvar křivek vytvořených koncem vektoru intenzity elektrického pole tvoří tvar Lissajousových křivek.
Podívejme se nejprve na speciální případ, kdy jsou obě ortogonální komponenty ve fázi. V tomto případě jsou obě komponenty stále stejné či v konstantním poměru, takže směr vektoru elektrického pole bude stále stejný v rovině kolmé na směr šíření. Tento stav nazýváme lineární polarizace. Směr vektoru je dán velikostí amplitud obou složek, může být skloněn v libovolném směru, ale ten se nemění. Na obrázku jsou červeně zachyceny některé vektory, jejich vrcholy jsou na sinusoidě (zelená barva). Modře je její průmět do roviny kolmé na směr pohybu.
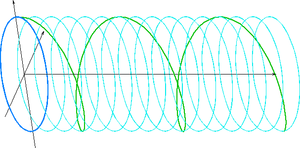
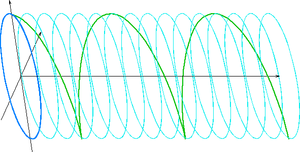
Pokud mají obě složky stejnou amplitudu, ale jejich fázový rozdíl je π/2 radiánů (90°), pak je jedna komponenta nulová, když druhá nabývá minima či maxima (její absolutní hodnota nabývá maxima). Existují dvě možnosti jak toto realizovat. Komponenta x může být o π/2 před či za komponentou y. Elektrický vektor složený z těchto komponent rovině kolmé na směr pohybu bude kroužit po kružnici. Tento stav nazýváme kruhovou polarizací a její dva stavy pravotočivá kruhová polarizace a levotočivá kruhová polarizace. Na obrázku je zeleně zaznačen vývoj umístnění vrcholu elektrického vektoru (opět vychází z osy z a jsou na ni kolmé), modře je naznačena stěna válce na níž jsou všechny vrcholy. Podstava válce je shodná s průmětem vektorů do roviny kolmé na směr šíření.
Všechny ostatní případy polarizovaného světla, kde obě komponenty nejsou ve fázi, ani nemají fázový rozdíl π/2 nebo nemají stejnou amplitudu, se nazývají eliptická polarizace neboť výsledný vektor vykružuje (polarizační) elipsu.
Nekoherentní záření
Mnoho běžného záření je produkované množstvím nezávislých světelných zdrojů. Jimi produkované světlo se zve nekoherentní. Obecně nemají společnou frekvenci, ale spíše spektrum nezávislých frekvencí. A i když vyfiltrujeme jen úzkou rozmezí frekvencí stálou, neměnnou polarizaci. To však neznamená, že by polarizace byla vlastností jen koherentního záření. Inkoherentní záření může jevit statistickou korelaci mezi komponentami elektrického pole, jež můžeme interpretovat jako částečnou polarizaci. Můžeme ji popsat i jako superpozici plně polarizovaného a nepolarizovaného.
Popis polarizace
Polarizaci obvykle popisujeme pomoci polarizační elipsy, zejména podle směru její hlavní poloosy a excentricity. Běžně se popisuje pomocí úhlu mezi hlavní poloosou a osou x a poměru délky poloos. Toto se užívá při geometrickém popisu polarizace, který má jen omezené využití Celkovou informaci o stavu polarizace získáme také pomocí amplitud a fáze ortogonálních složek vektoru elektrického pole v rovině polarizace, jak bylo použito výše. Informace o amplitudě a fázi bývají reprezentovány pomocí dvojdimenzionálního komplexního vektoru zvaného Jonesův vektor:
- \( \mathbf{e} = \begin{bmatrix}
a_1 e^{i \theta_1} \\ a_2 e^{i \theta_2} \end{bmatrix} .\) Všimněte si, že vynásobení komplexní jednotkou se nezmění stav polarizace, daný její elipsou, ale jen elektrické pole o danou část fáze, kterou dané číslo reprezentuje. Elektrické pole závisí na fázi, ale polarizace nikoli. Povšimněte si. že báze vektorů pro representaci Jonesova vektoru nemusí representovat lineární stavy polarizace (nemusí být reálná). Obecně mohou posloužit jakékoli dva ortogonální stavy, ortogonální vektory jsou definovány tak, že mají nulový skalární součin. Častou volbou je pravo- a levotočivá kruhová polarizace pro model jejich odlišného šíření v opticky aktivních látkách. Nehledě na to, zda polarizační elipsu popisujeme geometricky či pomocí maticově, máme volnost v tom, jak si zvolíme směr souřadnicových os. Ty můžeme prakticky libovolně rotovat podél směru pohybu záření. To nám umožní zvolit si souřadnice s významem pro pozorovatele. Například pozorujeme-li záření souběžné se zemským povrchem, obvykle se používá termínů horizontální a vertikální mód, kde druhý vyjadřuje módu kolmý na zemský povrch. Naopak v astronomii se používá rovníkový souřadný systém. Další systém se používá při studiu odrazu. Jak je zobrazeno na obrázku, mód TE se nazývá transverzálně elektrický nebo ortogonální, neboť elektrická pole jsou ortogonální k rovině dopadu, mód TM transverzálně magnetický (TM), neboť magnetická pole jsou ortogonální k rovině dopadu Alternativní pojmenování pro TM mód je paralelní, elektrické pole je paralelní s rovinou dopadu. V případě částečně polarizovaném záření Jonesův vektor se mění v čase i prostoru. V tomto případě je vlnové pole spíše stochastická a můžeme získat jen statistické údaje o korelaci mezi složkami. Tuto informaci vyjadřujeme pomocí koherenční matice:
- \( \begin{matrix}
\mathbf{\Psi} &=& \left\langle\mathbf{e} \mathbf{e}^\dagger \right\rangle \\
&=& \left\langle\begin{bmatrix}
e_1 e_1 & e_1 e_2^* \\
e_2 e_1^* & e_2 e_2
\end{bmatrix} \right\rangle \\
&=& \left\langle\begin{bmatrix}
a_1^2 & a_1 a_2 e^{i (\theta_1-\theta_2)} \\
a_1 a_2 e^{-i (\theta_1-\theta_2)}& a_2^2
\end{bmatrix} \right\rangle
\end{matrix}\) , kde lomené závorky vyjadřují průměr přes mnoho period.
Šíření, lom a rozptyl
Ve vakuu se elektrické pole šíří rychlostí světla, přičemž se mění fáze vlny, ale stav polarizace se nemění. Popisujeme to rovnicí:
- \( \mathbf{e}(z+\Delta z,t+\Delta t) = \mathbf{e}(z, t) e^{i k (c\Delta t - \Delta z)},\)
kde k je vlnové číslo a z je vzdálenost ve směr pohybu. Jak již bylo řečeno výše reálná část Jonesova vektoru vyjadřuje amplitudu elektrického pole. Když elektromagnetické vlny interagují s látkou, vlastnosti jejich šíření se mění. Pokud to závisí na stavu polarizace, mění se i ta. V mnoha typech látek dochází k rozkladu na dvě na sebe kolmé složky, které se šíří odlišně. K podobné situaci dochází i během zpracovávání signálů v detekčních zařízeních, jež zaznamenávají elektrické pole přímo. Šíření paprsku se dá vhodně popsat pomocí transformace popsané maticí 2×2 zvané Jonesova matice:
- \(\mathbf{e'} = \mathbf{J}\mathbf{e}.\)
Obecně Jonesova matice prostředí závisí na frekvenci vlny. Pro šíření dvou ortogonálních módů, můžeme Jonesovu matici psát: \(\mathbf{J} = \mathbf{T} \begin{bmatrix} g_1 & 0 \\ 0 & g_2 \end{bmatrix} \mathbf{T}^{-1}\), kde g1 a g2 jsou komplexní čísla udávající změnu amplitudy a fáze daného módu, a T je unitární matice reprezentující změnu báze z námi zvolené báze šíření záření na bázi danou vlastností prostředí. Pro ta prostředí, v nichž se nemění amplituda, ale dochází ke změně fázového rozdílu mezi složkami, je Jonesova matice unitární. Pokud se mění jen amplituda, je Jonesova matice hermitovská. Neboť „každá“ matice lze zapsat jako součin unitární a hermitovské matice, každé lineární šíření lze popsat jako součin těchto dvou typů transformací.
Média, ve kterých dochází k posunu fází složek dochází, se nazývají dvojlomná. Dobře známou ukázkou tohoto jevu jsou fázové destičky, Faradayova rotace a optická aktivita. Snadno představitelný případ je, kdy máme dva lineární módy a přicházející světlo je polarizováno v úhlu 45° k nim, jak světlo prochází mění se jeho polarizace na eliptickou, při posunutí o 90° na kruhovou, pak znovu eliptickou, při fázovém posunu 180° je lineárně polarizovaná kolmo ke vstupující vlně. Potom znovu přes stavy eliptické a kruhové polarizace se vrátí do původního stavu a cyklus může začít znovu. Media, v nichž se rozdílně mění amplituda složek, nazýváme dichroická. Optické prvky jež téměř nepropouštějí jednu složku se nazývají polarizační filtry nebo polarizátory.
Malusův pokus
K polarizaci světla může dojít odrazem nebo lomem světla. Světlo dopadající na rozhraní dvou prostředí se rozděluje na vlnu odraženou a vlnu lomenou. Každá z těchto vln se polarizuje. Polarizaci odrazem lze demonstrovat Malusovým pokusem.
Pokud dopadá světelný paprsek na skleněnou desku pod úhlem 56.5°, bude se při otáčení skleněné desky kolem směru dopadajícího paprsku odrážet stále stejně. Pokud však bude světlo odražené od této skleněné desky znovu dopadat na další desku (opět pod úhlem 56.5°), pak se světlo nebude odrážet stejně, pokud budeme touto druhou skleněnou deskou otáčet kolem směru paprsku, který na ni dopadá. Výsledný paprsek bude nejsilnější, pokud budou obě desky uspořádány rovnoběžně (viz a), pokud budou zkříženy, paprsek vymizí (viz b).
Malusův pokus lze vysvětlit na základě elektromagnetické teorie. Podle této teorie budou v odraženém světle převládat kmity v rovině kolmé k rovině dopadu, zatímco v lomeném světle budou převládat kmity ležící v rovině dopadu. Pro určitý speciální úhel \(\alpha_p\) lze odražené světlo považovat za zcela polarizované. Úhel \(\alpha_p\) se nazývá polarizační úhel.
Malusův zákon
Malusovy pokusy vedly k formulaci tzv. Malusova zákona, který říká, že pokud je ideální polarizační filtr umístěn do paprsku světla s intenzitou \(I_0\), pak světlo má po průchodu tímto polarizačním filtrem intenzitu
- \(I = I_0 \cos^2 \theta_i \,\),
kde \(I_0\) je počáteční intenzita světla a \(\theta_i\) je úhel mezi rovinou polarizace světelného paprsku a osou polarizačního filtru. Paprsek nepolarizovaného světla lze chápat jako složený z lineárně polarizovaných paprsků v různých směrech, přičemž žádný ze směrů není privilegovaný. Vzhledem k tomu, že průměrná hodnota \(\cos^2\theta\) je rovna \(\frac{1}{2}\), bude platit
- \(\frac {I}{I_0} = \frac {1}{2}\quad\)
Polarizace v přírodě, vědě a technologiích
Polarizace v každodenním životě
Každé světlo odražené od rovinného předmětu je alespoň částečně polarizované. Můžete to pozorovat za pomoci polarizačního filtru, který budete držet kolmo k rovině odrazu. Intenzita světla by se měla snížit. Filtr nepropouští světlo polarizované kolmo k jeho módu. Proto můžete položit dva filtry pootočené o 90° a nebude jimi procházet žádné světlo.
Polarizaci můžeme pozorovat všude kolem nás. Stačí si vzít jednoduchý polarizační filtr a otáčet s ním. Pokud na něj dopadá polarizované světlo mění se jas jim prošlého světla. Polarizaci můžeme pozorovat na světle procházejícím oblohou (dochází zde k jeho rozptylu). Fotografové vědí, že tato částečná polarizace způsobuje bledou oblohu na snímcích I lidské oko je slabě citlivé na polarizaci bez nutnosti použití filtrů, viz Haidingerův snop.
Biologie
Mnoho živočichů je schopno pozorovat polarizaci slunečního světla, což obvykle využívají pro navigaci, neboť polarizace slunečního světla procházejícího atmosférou je lineární a vždy kolmá ke směru, kde je slunce. Tato schopnost je častá mezi hmyzem, například včelami, které tuto informaci využívají pro orientaci tance, kterým sdělují, kde je potrava. Africký chrobák Scarabaeus zambesianus je také citlivý na polarizaci, ale na rozdíl od ostatních se orientuje pomocí polarizovaného světla Měsíce. Vnímavost polarizace byla též pozorována u chobotnice, sépie a strašilky. Sépie užívají rychle se měnící výrazné obrazce na pokožce ke komunikaci, přičemž některé vzory jsou polarizované. Od strašilek se světlo odráží rozdílně dle polarizace. Polarizaci oblohy mohou vnímat někteří obratlovci, například holub, pro kterého je to jedna, ale ne jediná, ze schopností umožňujících mu navádění.
Geologie
Dvojlom je rozšířená vlastnost mezi krystalickými minerály a byla tou, která vedla k objevení polarizace. V mineralogii se určují minerály i za pomoci polarizačního mikroskopu. Viz Pleochroismus.
Chemie
V chemii se využívá (kruhového) dichroismu a „optická rotace“ (kruhový dvojlom) jež pozorujeme u opticky aktivních (chirálních) molekul.
Technologie
Technologické využití je velmi široké. Asi nejčastějším využitím jsou LCD monitory. Všechny rádiové vysílače a přijímače jsou polarizované, speciální využití to má u radarů. Vztah mezi mechanickým napětím a dvojlomem se občas využívá k nalezení rozložení napětí v prototypech. Elektronicky kontrolované dvojlomné přístroje jsou spolu s polarizačními filtry využívány jako modulátory ve vlnovodné optice. Polarizace oblohy je využívaná v „sky compass“, který byl použit v padesátých letech dvacátého století při navigování v blízkosti zemského magnetického pólu, když nebylo vidět ani slunce, ani hvězdy (při denní oblačnosti či stmívání). Je sporná domněnka, že Vikingové využívali podobný přístroj („sunstone“) při jejich daleký cestách severním Atlantikem v 9. až 11. století, před příchodem magnetického kompasu do Evropy ve 12. století. Vztah k sky compass má „polar clock“, vynalezený Charlesem Wheatstonem koncem 19. století.
Související články
Externí odkazy
- Polarizace světla hranolem; polarizační hranol (Nicolův hranol, nikol): [1]
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |