Gaussův integrál

Z Multimediaexpo.cz

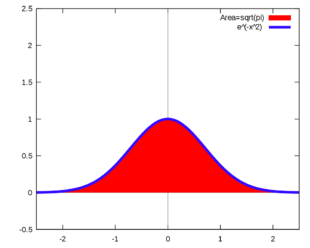
Gaussův integrál, také známý jako Eulerův-Poissonův integrál či Poissonův integrál,^[1] je integrál Gaussovy funkce e^−x2 přes celou reálnou osu, tedy

${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{e}^{-x^2}dx=\sqrt{\pi }.$

Jména tomuto integrálu dali matematici Carl Friedrich Gauss, Leonhard Euler a Siméon Denis Poisson.

Výpočet

Integrál Gaussovy funkce označíme $Y$.

$Y={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\mathrm{e}}^{-x^2}\mathrm{d}x$

Obě strany rovnice umocníme na druhou, přičemž proměnnou ve druhém integrálu označíme $y$.

$Y^2={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\mathrm{e}}^{-x^2}\mathrm{d}x{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\mathrm{e}}^{-y^2}\mathrm{d}y$

Součin integrálů odpovídá dvojnému integrálu funkce dvou proměnných, která je součinem původních funkcí.

$Y^2={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\mathrm{e}}^{-x^2}{\mathrm{e}}^{-y^2}\mathrm{d}x\mathrm{d}y={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\mathrm{e}}^{-(x^2+y^2)}\mathrm{d}x\mathrm{d}y$

Graf této funkce si můžeme představit jako kopec (tvarem připomíná horu Říp) nad rovinou s kartézskými souřadnicemi $(x,y)$. Integrál představuje objem kopce. Jelikož je kopec souměrný podle svislé osy, hodí se k jeho popisu polární soustava souřadnic $(\phi ,r)$, do kterých funkci přepíšeme.

$Y^2={\int }_0^{2\pi }{\int }_0^{\mathrm{\infty }}r{\mathrm{e}}^{-r^2}\mathrm{d}\phi \mathrm{d}r={\int }_0^{2\pi }\mathrm{d}\phi {\int }_0^{\mathrm{\infty }}r{\mathrm{e}}^{-r^2}\mathrm{d}r$

Tento integrál už lze jednoduše vyčíslit nalezením primitivní funkce metodou per partes a jeho hodnota je $\pi$. Odmocněním rovnice dostaneme výsledek.

$Y=\sqrt{\pi }$

Reference

1. ↑ Пуассона интеграл, БСЭ

Externí odkazy

• Kvasnica J.: Matematický aparát fyzika

[zobrazit] Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010
Informace o článku. Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. Tento text je dostupný za podmínek Creative Commons 3.0 Unported – creativecommons.org. Originální článek na české Wikipedii