V sobotu 2. listopadu proběhla mohutná oslava naší plnoletosti !!
Multimediaexpo.cz je již 18 let na českém internetu !!
V tiskové zprávě k 18. narozeninám brzy najdete nové a zásadní informace.

Newtonův gravitační zákon

Z Multimediaexpo.cz

(Rozdíly mezi verzemi)
(Články s oknem do Wikipedie)
m (Nahrazení textu „</math>“ textem „\)</big>“)
 
(Nejsou zobrazeny 3 mezilehlé verze.)
Řádka 1: Řádka 1:
-
{{Wikipedia-cs|Newtonův gravitační zákon|700}}
+
[[Soubor:NewtonsLawOfUniversalGravitation.png|thumb|250px|Newtonův gravitační zákon graficky]]
 +
'''Newtonův gravitační zákon''' je fyzikální [[Vědecký zákon|zákon]], který popisuje [[Gravitace|gravitaci]] jako přitažlivou [[síla|sílu]] – '''gravitační sílu''', kterou na sebe působí [[Těleso|tělesa]] v závislosti na svých [[hmotnost]]ech a vzájemné vzdálenosti.
 +
 
 +
Formuloval jej Isaac&nbsp;Newton (1642–1727) na základě analýzy [[Mechanický pohyb|pohybu]] [[Měsíc]]e kolem [[Země]], [[planeta|planet]] kolem [[Slunce]] a na základě znalosti [[Keplerovy zákony|Keplerových zákonů]].
 +
 
 +
Newtonův gravitační zákon je důležitou částí [[klasická fyzika|klasické fyziky]]. Není však vhodný pro velmi hmotné vesmírné objekty a [[rychlost]]i blížící se [[rychlost světla|rychlosti světla]], pro které platí přesnější a složitější definice gravitace [[obecná teorie relativity|obecné teorie relativity]]. [[Kvantová gravitace|Kvantovou teorii gravitace]] se zatím nepodařilo vytvořit.
 +
 
 +
== Formulace zákona ==
 +
Každá dvě tělesa o [[hmotnost]]ech <big>\(m_1\)</big> a <big>\(m_2\)</big>, která můžeme dostatečně přesně [[aproximace|aproximovat]] [[hmotný bod|body]], nebo jsou sféricky symetrická (jak vyplývá z&nbsp;[[gaussova věta|Gaussovy věty]]) na sebe působí gravitační silou přímo úměrnou ''[[hmotnost]]em'' těles a nepřímo úměrnou čtverci jejich ''[[vzdálenost]]i''
 +
:<big>\(F_g = G { m_1 m_2 \over r^2}\,\)</big>,
 +
kde G (dříve značeno <big>\(\kappa\)</big>) je [[gravitační konstanta]] s hodnotou (přibližně) 6,67×10<sup>−11</sup> [[metr|m]]<sup>3</sup>·[[kilogram|kg]]<sup>-1</sup>·[[sekunda|s]]<sup>-2</sup>, ''m''<sub>1</sub> je hmotnost prvního hmotného bodu, ''m''<sub>2</sub> je hmotnost druhého hmotného bodu a ''r'' je vzdálenost obou hmotných bodů.
 +
 
 +
[[Vektor]]ově lze vyjádřit např. sílu působící na 1. těleso)
 +
:<big>\(\mathbf{F}_1 = -G \frac{ m_1 m_2}{r^2} \frac{\mathbf{r}}{r}= m_1 \mathbf{K_2(\mathbf{r})}\)</big>,
 +
kde <big>\(\mathbf{r}\)</big> je [[polohový vektor]] (průvodič) 1. tělesa vzhledem ke druhému a <big>\(\mathbf{K_2}\)</big> intenzita gravitačního pole 2. tělesa v místě (středu) 1. tělesa. [[Vektor]] této [[Síla|síly]] leží na spojnici [[Těžiště|hmotných středů]] těchto těles - síla je [[Centrální síla|centrální]].
 +
 
 +
Pokud je rozložení [[hmota|hmoty]] udáno funkcí [[hustota|hustoty]] <big>\(\rho(\mathbf{r})\)</big> (a je tedy zcela obecné), pak je možné gravitační sílu, kterou takto rozložená hmota působí na [[testovací částice|testovací částici]] hmotnosti ''m,'' zapsat ve tvaru
 +
:<big>\(\mathbf{F}_g = -  G m \int_V{{\rho(\mathbf{r}') \over {|\mathbf{r}-\mathbf{r}'|^{3}}} (\mathbf{r}-\mathbf{r}')} \mathrm{d}V'\, = m \mathbf{K(\mathbf{r})}\)</big>.
 +
 
 +
Lze ukázat, že (obecné) centrální pole je vždy [[konzervativní pole|konzervativní]], takže zde existuje [[gravitační potenciál]] <big>\(\phi\)</big>
 +
 
 +
:<big>\(\mathbf{K(\mathbf{r})} = - \nabla \phi (r) = - \frac{\mathrm{d}\phi (r)}{\mathrm{d}r} \frac{\mathbf{r}}{r}\)</big>.
 +
 
 +
V&nbsp;gravitačním poli centrálního tělesa se testovací částice zanedbatelné hmotnosti (vůči hmotnosti centrálního tělesa) pohybují po [[kuželosečka|kuželosečkách]], tedy např. planety po [[elipsa|elipsách]] podle [[keplerovy zákony|Keplerových zákonů]].
 +
 
 +
Obecné [[Gravitace|gravitační pole]] je vždy [[konzervativní pole|konzervativní]].
 +
 
 +
== Homogenní pole ==
 +
Gravitační pole se nazývá '''[[homogenní gravitační pole|homogenní]]''', pokud jeho intenzita <big>\(\mathbf{K}\)</big> je v nějaké části prostoru konstantní (vektorově, co do velikosti i směru). Jeho [[siločáry]] jsou úsečky a potenciál lineární funkce (kartézských) souřadnic.
 +
 
 +
Podmínka [[homogenita|homogenity]] gravitačního pole je dostatečně přesně splněna například na povrchu [[Země]] či jiných planet (jimž přísluší jiné hodnoty [[gravitační zrychlení|gravitačního zrychlení]]).
 +
 
 +
== Tíhová síla a tíha ==
 +
{{viz též|Tíhové pole}}
 +
'''Tíhová síla''' je [[síla]], která působí na [[Těleso|tělesa]] na povrchu [[Země]] (přesněji ve vztažné soustavě spojené s povrchem Země či, v zobecněném případě, jiného tělesa). Je ''[[výslednice sil|výslednicí]]'' ''gravitační síly'' Země a ''[[Odstředivá síla|odstředivé síly]]'' vzniklé [[Otáčivý pohyb|otáčením]] Země kolem své [[osa otáčení|osy]].
 +
 
 +
Tíhová síla se mění se ''[[zeměpisná šířka|zeměpisnou šířkou]]'' a je vždy (až na póly) ''menší'' než gravitační síla a nemá (kromě na [[Zemský rovník|rovníku]] a na [[pól]]ech) s ní ani stejný směr. Rozdíl mezi tíhovou a gravitační silou není příliš velký a v běžných případech jej lze zanedbat.
 +
 
 +
Pole tíhové síly se nazývá ''tíhové pole''. Vektorem tíhové síly je určen svislý směr. Tíhová síla '''''F'''''<sub>G</sub> udílí všem tělesům v soustavě spojené s povrchem Země ''[[tíhové zrychlení]]'' '''''g''''', tedy zrychlení [[volný pád|volného pádu]] v daném místě.
 +
:<big>\(\mathbf{F}_\mathrm{G} = m \mathbf{g}\)</big>.
 +
 
 +
 
 +
'''[[Tíha]]''' je fyzikální veličina vyjadřující sílu, kterou v tíhovém poli působí těleso, nacházející se v dané soustavě v klidu, na podložku nebo závěs. Jedná se tedy o statický projev působící tíhové síly. Tíha '''''G''''' je proto stejně velká jako působící tíhová síla a má i stejný směr, liší se jen působištěm. Zatímco tíhová síla působí na těleso v jeho těžišti, tíhou působí těleso na závěs v místě upevnění nebo na podložku v místě, kde na ní leží.
 +
:<big>\(\mathbf{G} = \mathbf{F}_\mathrm{G}\)</big>
 +
 
 +
Pojem tíhy lze zobecnit i na jiné soustavy pohybující se vzhledem k povrchu Země (či jiného tělesa). Pak vyjadřuje statické působení tělesa v této soustavě, které vzniká jako výsledek gravitační síly a všech působících [[setrvačná síla|setrvačných sil]] daných pohybem soustavy. V tomto smyslu se pak u soustav s výsledným nulovým silovým působením hovoří o ''beztížném stavu'' a u soustav s tíhou větší než místní gravitační síla o ''přetížení''.
 +
 
== Související články ==
== Související články ==
* [[Gravitace]]
* [[Gravitace]]
Řádka 5: Řádka 51:
* [[Tíha]]
* [[Tíha]]
 +
== Externí odkazy ==
 +
 +
 +
{{Flickr|Gravitation}}{{Commonscat|Gravitation}}{{Článek z Wikipedie}}
[[Kategorie:Gravitace]]
[[Kategorie:Gravitace]]
 +
[[Kategorie:Fyzikální zákony]]

Aktuální verze z 14. 8. 2022, 14:52

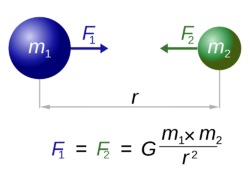
Newtonův gravitační zákon graficky

Newtonův gravitační zákon je fyzikální zákon, který popisuje gravitaci jako přitažlivou sílu – gravitační sílu, kterou na sebe působí tělesa v závislosti na svých hmotnostech a vzájemné vzdálenosti.

Formuloval jej Isaac Newton (1642–1727) na základě analýzy pohybu Měsíce kolem Země, planet kolem Slunce a na základě znalosti Keplerových zákonů.

Newtonův gravitační zákon je důležitou částí klasické fyziky. Není však vhodný pro velmi hmotné vesmírné objekty a rychlosti blížící se rychlosti světla, pro které platí přesnější a složitější definice gravitace obecné teorie relativity. Kvantovou teorii gravitace se zatím nepodařilo vytvořit.

Obsah

Formulace zákona

Každá dvě tělesa o hmotnostech \(m_1\) a \(m_2\), která můžeme dostatečně přesně aproximovat body, nebo jsou sféricky symetrická (jak vyplývá z Gaussovy věty) na sebe působí gravitační silou přímo úměrnou hmotnostem těles a nepřímo úměrnou čtverci jejich vzdálenosti

\(F_g = G { m_1 m_2 \over r^2}\,\),

kde G (dříve značeno \(\kappa\)) je gravitační konstanta s hodnotou (přibližně) 6,67×10−11 m3·kg-1·s-2, m1 je hmotnost prvního hmotného bodu, m2 je hmotnost druhého hmotného bodu a r je vzdálenost obou hmotných bodů.

Vektorově lze vyjádřit např. sílu působící na 1. těleso)

\(\mathbf{F}_1 = -G \frac{ m_1 m_2}{r^2} \frac{\mathbf{r}}{r}= m_1 \mathbf{K_2(\mathbf{r})}\),

kde \(\mathbf{r}\) je polohový vektor (průvodič) 1. tělesa vzhledem ke druhému a \(\mathbf{K_2}\) intenzita gravitačního pole 2. tělesa v místě (středu) 1. tělesa. Vektor této síly leží na spojnici hmotných středů těchto těles - síla je centrální.

Pokud je rozložení hmoty udáno funkcí hustoty \(\rho(\mathbf{r})\) (a je tedy zcela obecné), pak je možné gravitační sílu, kterou takto rozložená hmota působí na testovací částici hmotnosti m, zapsat ve tvaru

\(\mathbf{F}_g = - G m \int_V{{\rho(\mathbf{r}') \over {|\mathbf{r}-\mathbf{r}'|^{3}}} (\mathbf{r}-\mathbf{r}')} \mathrm{d}V'\, = m \mathbf{K(\mathbf{r})}\).

Lze ukázat, že (obecné) centrální pole je vždy konzervativní, takže zde existuje gravitační potenciál \(\phi\)

\(\mathbf{K(\mathbf{r})} = - \nabla \phi (r) = - \frac{\mathrm{d}\phi (r)}{\mathrm{d}r} \frac{\mathbf{r}}{r}\).

V gravitačním poli centrálního tělesa se testovací částice zanedbatelné hmotnosti (vůči hmotnosti centrálního tělesa) pohybují po kuželosečkách, tedy např. planety po elipsách podle Keplerových zákonů.

Obecné gravitační pole je vždy konzervativní.

Homogenní pole

Gravitační pole se nazývá homogenní, pokud jeho intenzita \(\mathbf{K}\) je v nějaké části prostoru konstantní (vektorově, co do velikosti i směru). Jeho siločáry jsou úsečky a potenciál lineární funkce (kartézských) souřadnic.

Podmínka homogenity gravitačního pole je dostatečně přesně splněna například na povrchu Země či jiných planet (jimž přísluší jiné hodnoty gravitačního zrychlení).

Tíhová síla a tíha

Tíhová síla je síla, která působí na tělesa na povrchu Země (přesněji ve vztažné soustavě spojené s povrchem Země či, v zobecněném případě, jiného tělesa). Je výslednicí gravitační síly Země a odstředivé síly vzniklé otáčením Země kolem své osy.

Tíhová síla se mění se zeměpisnou šířkou a je vždy (až na póly) menší než gravitační síla a nemá (kromě na rovníku a na pólech) s ní ani stejný směr. Rozdíl mezi tíhovou a gravitační silou není příliš velký a v běžných případech jej lze zanedbat.

Pole tíhové síly se nazývá tíhové pole. Vektorem tíhové síly je určen svislý směr. Tíhová síla FG udílí všem tělesům v soustavě spojené s povrchem Země tíhové zrychlení g, tedy zrychlení volného pádu v daném místě.

\(\mathbf{F}_\mathrm{G} = m \mathbf{g}\).


Tíha je fyzikální veličina vyjadřující sílu, kterou v tíhovém poli působí těleso, nacházející se v dané soustavě v klidu, na podložku nebo závěs. Jedná se tedy o statický projev působící tíhové síly. Tíha G je proto stejně velká jako působící tíhová síla a má i stejný směr, liší se jen působištěm. Zatímco tíhová síla působí na těleso v jeho těžišti, tíhou působí těleso na závěs v místě upevnění nebo na podložku v místě, kde na ní leží.

\(\mathbf{G} = \mathbf{F}_\mathrm{G}\)

Pojem tíhy lze zobecnit i na jiné soustavy pohybující se vzhledem k povrchu Země (či jiného tělesa). Pak vyjadřuje statické působení tělesa v této soustavě, které vzniká jako výsledek gravitační síly a všech působících setrvačných sil daných pohybem soustavy. V tomto smyslu se pak u soustav s výsledným nulovým silovým působením hovoří o beztížném stavu a u soustav s tíhou větší než místní gravitační síla o přetížení.

Související články

Externí odkazy

Flickr.com nabízí fotografie, obrázky a videa k tématu
Newtonův gravitační zákon
Commons nabízí fotografie, obrázky a videa k tématu
Newtonův gravitační zákon
Citováno z „http://ww.multimediaexpo.cz/mmecz/index.php/Newton%C5%AFv_gravita%C4%8Dn%C3%AD_z%C3%A1kon“