V sobotu 2. listopadu proběhla mohutná oslava naší plnoletosti !!
Multimediaexpo.cz je již 18 let na českém internetu !!
V tiskové zprávě k 18. narozeninám brzy najdete nové a zásadní informace.

Pohyb v centrálním gravitačním poli

Z Multimediaexpo.cz

Pohyb v centrálním gravitačním poli je pohyb v v centrálním gravitačním poli.

Pohyb v radiálním gravitačním poli je určován dvěma rychlostmi, první kosmickou rychlostí (Kruhová rychlost), což je rychlost pohybu po kruhové dráze kolem zdroje gravitační síly a druhá kosmická rychlost (Úniková rychlost), což je rychlost potřebná k úniku z gravitačního pole daného tělesa.

Příkladem pohybu v centrálním gravitčním poli je pohyb kolem nebeských těles.

Obsah

Pohyb v gravitačním poli Země

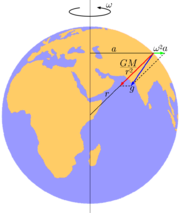
Ilustrace příspěvku gravitačních a odstředivých sil na gravitační zrychlení na zemi (velikost vektorů není proporční). M je hmotnost Země, G je gravitační konstanta.

Pohyb v gravitačním poli Země je pohyb, kdy se těleso pohybuje v centrálním gravitačním poli Země. Při pohybu tělesa kolem Země působí na těleso gravitační síla směrem do středu Země, její velikost závisí na hmotnosti tělesa a vzdálenosti od středu Země. Tato síla způsobí zakřivení trajektorie tělesa, jejímž důsledkem je vznik odstředivé síly.

Je-li velikost gravitační síly větší než velikost odstředivé síly, pak těleso dopadne na Zemi. Je-li velikost gravitační síly a odstředivé síly stejná, pak se těleso pohybuje po kruhové trajektorii. Je-li velikost gravitační síly menší než odstředivé síly, pak se těleso pohybuje po eliptické trajektorii (perigeum, apogeum) nebo může uniknout z dosahu zemské gravitace.

Při křivočarém pohybu vzniká odstředivá síla jako reakce na dostředivou gravitační sílu, která závisí na hmotnosti tělesa, poloměru zakřivení a na rychlosti tělesa.

Pohyb kolem Země po kružnici

  • těleso krouží kolem Země
  • perioda pohybu závisí na vzdálenosti od Země
  • vzdálenost od Země závisí na rychlosti tělesa
  • rychlost = 1. kosmická rychlost (kruhová rychlost)přibližně 7,9 km.s-1

Pohyb kolem Země po elipse

  • rychlost je větší než 1. kosmická rychlost a menší než 2. kosmická rychlost
  • výstřednost elipsy roste s velikostí rychlosti tělesa
  • v jednom ohnisku elipsy leží Země
  • nejmenší vzdálenost tělesa a Země se nazývá perigeum
  • největší vzdálenost tělesa a Země se nazývá apogeum

Pohyb kolem Země po parabole

  • rychlost = 2. kosmická rychlost (úniková rychlost) - přibližně 11,2 km.s-1,
  • těleso může uniknout z dosahu gravitace Země

Pohyb kolem Země po hyperbole

  • rychlost je větší než 2. kosmická rychlost
  • Země zakřiví trajektorii tělesa pohybující se kolem něj, ale těleso nezůstane v gravitačním poli Země

Tíhové zrychlení

Protože Země rotuje kolem své osy jedná se v podstatě o rotující neinerciální soustava a při popisu pozorovatele stojícího na zemi započítáváme i setrvačnost. Tedy na volně padající těleso působí celková síla 

F=Fg+Fo+Fc

Fg-gravitační síla ,Fo-odstředivá síla,Fc-coriolisova síla.

  • Na nehybnou věc coriolisova síla nepůsobí. 
G=Fg +Fo
  • této síle říkáme tíha.
  • To čemu se říká tíhové zrychlení je součet intenzity gravitačního pole K a odstředivého zrychlení. 
g=G/m=K+aO

g je přibližně 10 m/s. Z toho spočteme odstředivé zrychlení. Pokud se otáčí Země za hvězdný den T (o 4 min kratší než normální), je Úhlová rychlost rovna 

Ώ=2π/T

to je asi 7,3 krát 10-5 s-1, může se zdát, že se jedná o malou rychlost, ale rotaci Země odpovídá na rovníku obvodová rychlost 

v=ΏRz

asi 460m/s (1700km/h), což je o 40 procent víc než je rychlost zvuku, takže odstředivé zrychlení (na rovníku) je 

ao=Ώ2Rz

asi 3,4 krát 10-2 m/s2. Odstředivé zrychlení tvoří 3 promile z tíhového zrychlení.

Mezinárodní vzorec pro tíhové zrychlení u hladiny moře 

g=ge(1 + ϒ2 sin2ο+ϒ4sin4ο)

ge=9,78032m/s2 tíhové zrychlení na rovníku, ο- zeměpisná šířka, ϒ2 =0,005278 a ϒ4 = 0,000023 jsou korekční koeficienty ge=9,78 m/s2na rovníku a na pólech ge=9,81 m/s2.

Tvar Země

Pokud bychom Zemi pokládali za nehybnou kouli, měla by tíha směřovat do středu Země. Díky otáčení Země tento se směr vektoru tíha odklání od středu Země. Měla by být rovna 

(Ώ2Rz/2g)*sin 2ο

výsledek je matematicky 6 vteřin, ale je experimentálně je zjištěno 11, důvodem je, že střed Země je tekutý. Díky deformaci odstředivých sil je nemá Země tvar koule ale spíše rotačního elipsoidu.

Coriolisova síla a rotace Země

Pohyb těles ve vertikální rovině je řízen gravitací ,ale v horizontální rovině se gravitace těles neuplatní, takže tělesa by se měla pohybovat podle zákona setrvačnosti.Pokud uvážíme coriolisovu sílu zjistíme ,že zákon setrvačnosti neplatí ani pro horizontální pohyby.Pokud omezíme obecný vzorec pro coriolusovu sílu pouze na horizontální rovinu,vyplývá že Corioliesova síla je kolmá na na rychlost pohybu a proto na severní polokouli směřuje vždy napravo od směru pohybu,na jižní opačně a na rovníku se tato síla neprojeví vůbec. Proto jsou víry na WC při spláchnutí /viz díl Simpsonových:-)/ na severní polokouli proti směru hodinových ručiček a na jižní opačně.Podobně platí že díky coriolisově síle je na severní polokouli víc podemletý a strmější pravý břeh řeky. Na jižní naopak.

Zajímavosti

  • Statistiky pojišťoven ukazují,že na severní polokouli vlaky častěji vykolejují na pravou stranu než na levou.
  • středověká věda nikdy neuznala tak rychlou rotaci planety
  • Tíhové zrychlení klesá s nadmořskou výškou protože se vzdalujeme od středu Země asi o 0,003 m/s2 na každý kilometr.
  • Někoho by mohlo napadnout jestli neovlivňuje tíhové zrychlení také Slunce. Odstředivá síla Slunce je plně kompenzována silou kterou nás Slunce přitahuje.

Pohyb tělesa kolem Slunce

Pohyb tělesa kolem Slunce je pohyb, kdy se těleso pohybuje v centrálním gravitačním poli Slunce. Nejčastěji se jedná o pohyb planet, komet a jiných objektů ve Sluneční soustavě.

Pohyb tělesa ovlivňují především gravitační síla Slunce, která míří do středu Slunce, a odstředivá síla, která vzniká při křivočarém pohybu těles a má směr opačný než gravitační síla.

Planety se kolem Slunce pohybují většinou po eliptických trajektoriích, pro jejich pohyb platí Keplerovy zákony.

Trajektorie komet mají tvar velmi výstředné elipsy blížící se parabole. Jejich rychlost se zvyšuje, když se blíží ke Slunci, a zmenšuje, když se od Slunce vzdalují.

Úniková rychlost z dosahu gravitace Slunce je při povrchu Slunce 620 km.s-1, dál od Slunce je tato rychlost menší, ve vzdálenosti 1 AU (ve vzdálenosti Země od Slunce) je úniková rychlost 16,3 km.s-1.

Nejbližší místo ke Slunci, kterým těleso při svém pohybu prochází, se nazývá perihelium (přísluní), nejvzdálenější místo od Slunce se nazývá afélium (odsluní).

Související články

Externí odkazy

Citováno z „http://ww.multimediaexpo.cz/mmecz/index.php/Pohyb_v_centr%C3%A1ln%C3%ADm_gravita%C4%8Dn%C3%ADm_poli“