Geometrický útvar
Z Multimediaexpo.cz
m (Nahrazení textu „<math>“ textem „<big>\(“) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| Řádka 47: | Řádka 47: | ||
| jazyk = | | jazyk = | ||
}}</ref> popř. i sám [[Prostor (geometrie)|prostor]].<ref name="BARTSCH"/> Mezi základní geometrické útvary se někdy zahrnují i jiné útvary; ve [[výuka matematiky|školské matematice]] například [[kružnice]], [[trojúhelník]] nebo [[čtverec]]. | }}</ref> popř. i sám [[Prostor (geometrie)|prostor]].<ref name="BARTSCH"/> Mezi základní geometrické útvary se někdy zahrnují i jiné útvary; ve [[výuka matematiky|školské matematice]] například [[kružnice]], [[trojúhelník]] nebo [[čtverec]]. | ||
| - | ** Bod je bezrozměrný dále nedělitelný element. Body se v učebnicích často značí velkými písmeny <big>\(A</ | + | ** Bod je bezrozměrný dále nedělitelný element. Body se v učebnicích často značí velkými písmeny <big>\(A\)</big>, <big>\(B\)</big>, <big>\(C\)</big>,… |
| - | ** Přímka je abstrakce rovné čáry nulové šířky, jednorozměrný objekt, označuje se malým písmenem <big>\(a</ | + | ** Přímka je abstrakce rovné čáry nulové šířky, jednorozměrný objekt, označuje se malým písmenem <big>\(a\)</big>, <big>\(b\)</big>, <big>\(p\)</big>, <big>\(q\)</big> nebo <big>\(\overline{A B}\)</big> pomocí dvou různých bodů, které ji určují. |
| - | ** Rovina je abstrakce ploché rovné desky nulové tloušťky, značí se písmeny řecké abecedy <big>\(\alpha</ | + | ** Rovina je abstrakce ploché rovné desky nulové tloušťky, značí se písmeny řecké abecedy <big>\(\alpha\)</big>, <big>\(\beta\)</big>, <big>\(\rho\)</big>, <big>\(\pi\)</big>, nebo také <big>\(\overline{A B C}\)</big> pomocí tří různých bodů neležících na jedné přímce, které ji určují. |
* V hilbertovské axiomatizaci geometrie se jsou bod, přímka a rovina spolu s některými vlastnostmi a vzájemnými vztahy definovány axiomaticky a další vlastnosti, útvary a tvrzení se odvozují z těchto stavebních prvků. | * V hilbertovské axiomatizaci geometrie se jsou bod, přímka a rovina spolu s některými vlastnostmi a vzájemnými vztahy definovány axiomaticky a další vlastnosti, útvary a tvrzení se odvozují z těchto stavebních prvků. | ||
* V [[počítačová grafika|počítačové grafice]] se můžeme setkat s termínem [[grafické primitivum]], což obvykle [[křivka]], [[Mnohoúhelník|polygon]] a podobně. | * V [[počítačová grafika|počítačové grafice]] se můžeme setkat s termínem [[grafické primitivum]], což obvykle [[křivka]], [[Mnohoúhelník|polygon]] a podobně. | ||
| Řádka 71: | Řádka 71: | ||
=== Podle stupně polynomu === | === Podle stupně polynomu === | ||
[[Analytická geometrie]] dělí útvary a své subdisciplíny podle stupně [[polynom]]ů, popisujících útvar:<ref>Kol.: ''Aplikovaná matematika 1'', SNTL, Praha 1977, s. 83–84</ref> | [[Analytická geometrie]] dělí útvary a své subdisciplíny podle stupně [[polynom]]ů, popisujících útvar:<ref>Kol.: ''Aplikovaná matematika 1'', SNTL, Praha 1977, s. 83–84</ref> | ||
| - | * [[Analytická geometrie lineárních útvarů|Analytická geometrie '''lineárních útvarů''']] se zabývá útvary popsatelnými ve vhodně zvolené souřadné soustavě [[polynom]]y prvního stupně (v nichž souřadnice vystupují v první mocnině); příkladem je [[přímka]] (lze v rovině popsat rovnicí tvaru <big>\(y = a x + b</ | + | * [[Analytická geometrie lineárních útvarů|Analytická geometrie '''lineárních útvarů''']] se zabývá útvary popsatelnými ve vhodně zvolené souřadné soustavě [[polynom]]y prvního stupně (v nichž souřadnice vystupují v první mocnině); příkladem je [[přímka]] (lze v rovině popsat rovnicí tvaru <big>\(y = a x + b\)</big>, v prostoru soustavou <big>\(b c(x - x_0) = a c(y - y_0) = a b(z-z_0)\)</big>) či [[rovina]] (lze v prostoru popsat rovnicí tvaru <big>\(a x + b y + c z + d = 0\)</big>). |
| - | * [[Analytická geometrie kvadratických útvarů|Analytická geometrie '''kvadratických útvarů''']] se zabývá útvary popsatelnými ve vhodně zvolené souřadné soustavě polynomy druhého stupně (v nichž jedna nebo více souřadnic vystupuje v druhé mocnině); příkladem jsou v rovině [[kuželosečka|kuželosečky]] (např. [[parabola (matematika)|parabolu]] lze popsat rovnicí tvaru <big>\(y = a x^2 + b x + c</ | + | * [[Analytická geometrie kvadratických útvarů|Analytická geometrie '''kvadratických útvarů''']] se zabývá útvary popsatelnými ve vhodně zvolené souřadné soustavě polynomy druhého stupně (v nichž jedna nebo více souřadnic vystupuje v druhé mocnině); příkladem jsou v rovině [[kuželosečka|kuželosečky]] (např. [[parabola (matematika)|parabolu]] lze popsat rovnicí tvaru <big>\(y = a x^2 + b x + c\)</big>), v prostoru [[kvadrika|kvadriky]] (např. [[paraboloid#Hyperbolický paraboloid|hyperbolický paraboloid]] lze popsat rovnicí <big>\(z-z_0 = (1/2p)(x- x_0)^2 - (1/2q)(y-y_0)^2\)</big>, kde <big>\(pq > 0 \)</big>). |
* [[Algebraická geometrie]] se zabývá útvary popsatelnými polynomy obecného stupně. | * [[Algebraická geometrie]] se zabývá útvary popsatelnými polynomy obecného stupně. | ||
| Řádka 91: | Řádka 91: | ||
Kromě obecných [[matematická logika|logických]] vztahů ([[existence]], [[rovnost (matematika)|rovnost]]) používá Hilbertovská axiomatizace geometrie tři různé vztahy mezi geometrickými objekty:<ref>Aplikovaná matematika 1, s. 420–422</ref> | Kromě obecných [[matematická logika|logických]] vztahů ([[existence]], [[rovnost (matematika)|rovnost]]) používá Hilbertovská axiomatizace geometrie tři různé vztahy mezi geometrickými objekty:<ref>Aplikovaná matematika 1, s. 420–422</ref> | ||
| - | # Incidence, což znamená vlastnost „ležet na“, „ležet v“, „být prvkem“. Značí se <big>\(\in</ | + | # Incidence, což znamená vlastnost „ležet na“, „ležet v“, „být prvkem“. Značí se <big>\(\in\)</big> a její negace jako <big>\({\not \in}\)</big>. Například <big>\(A\in p\)</big> znamená „bod ''A'' leží na přímce ''p''“. |
# Vlastnost „ležet mezi“, např. bod ''A'' leží mezi body ''X'' a ''Y'' na přímce ''p''. | # Vlastnost „ležet mezi“, např. bod ''A'' leží mezi body ''X'' a ''Y'' na přímce ''p''. | ||
| - | # [[Shodnost]], tedy schopnost útvarů se po vhodné transformaci zachovávající vzdálenosti ztotožnit. Týká se např. úseček (stejná délka) nebo úhlů (stejná velikost úhlu). Značí se <big>\(\cong</ | + | # [[Shodnost]], tedy schopnost útvarů se po vhodné transformaci zachovávající vzdálenosti ztotožnit. Týká se např. úseček (stejná délka) nebo úhlů (stejná velikost úhlu). Značí se <big>\(\cong\)</big>. Například <big>\(\triangle \mathrm{ABC} \cong \triangle \mathrm{DEF}\)</big> čteme „trojúhelník ABC je shodný s trojúhelníkem DEF“ a znamená to, že oba trojúhelníky mají stejné délky stran a velikosti úhlů. |
Vedle shodnosti existují další [[Geometrické zobrazení|geometrická zobrazení]], zejména [[podobnost (geometrie)|podobnost]], [[afinní zobrazení]] a [[topologické zobrazení|topologická zobrazení]]. Jelikož útvary jsou množiny, je možno o nich také hovořit množinovým jazykem a zkoumat například jejich [[průnik]] a [[sjednocení]]. | Vedle shodnosti existují další [[Geometrické zobrazení|geometrická zobrazení]], zejména [[podobnost (geometrie)|podobnost]], [[afinní zobrazení]] a [[topologické zobrazení|topologická zobrazení]]. Jelikož útvary jsou množiny, je možno o nich také hovořit množinovým jazykem a zkoumat například jejich [[průnik]] a [[sjednocení]]. | ||
Aktuální verze z 14. 8. 2022, 14:51
Geometrický útvar je souhrn geometrických objektů, nejčastěji bodů, přímek či rovin.[1] Někdy se geometrický útvar definuje přímo jako množina bodů Euklidova prostorů,[2][3] ačkoliv ty samé zdroje uvádějí jako geometrický útvar i samotný bod (tedy prvek).[2] Podle této definice je tedy například čtverec společný název pro nekonečně mnoho různých geometrických útvarů. Jiné zdroje popisují geometrický útvar jako to, co je charakterizováno tvarem dané množiny, který se nemění u otočení a posunutí.[4][5][6] V Ottově slovníků naučném je geometrický útvar popsán jako matematický objekt, který zachycuje tvar, velikost a polohu tělesa, nehledíce ale k jeho hmotě.[7] Často se slovní spojení geometrický útvar používá také pro typ geometrického objektu, který je pojmenován (například bod, přímka, prostor,[2] ale také trojúhelník nebo čtverec[8]).
Další příklady geometrických útvarů jsou křivka, prostorový úhel, mezikruží či fraktál. Uzavřenou oblast v rovině nazýváme obrazcem, v prostoru tělesem.[2]
Jednoduché geometrické útvary byly známy již v paleolitu a podrobněji zkoumány ve všech antických civilizacích. Na vědecké úrovni se jim poprvé věnovali staří Řekové jako Eukleidés a další. V raném novověku René Descartes vynalezl souřadnice, což umožnilo vznik analytické geometrie a zkoumání útvarů algebraickými prostředky. 19. století postavilo matematiku na nové formální základy, z hlediska geometrie byl významný například vznik neeukleidovské geometrie a teorie množin.
Útvary ve třírozměrném prostoru se dělí na rovinné (rovinné křivky a obrazce) a prostorové (prostorové křivky, plochy v prostoru a tělesa). V analytické geometrii se vydělují lineární a kvadratické geometrické útvary podle stupně polynomu, který je popisuje. K základním vlastnostem útvarů patří jejich míra (délka, obsah, objem, povrch či obvod), dimenze, symetrie, souvislost nebo konvexnost. Geometrie zkoumá také vztahy mezi útvary, jako jsou shodnost, podobnost a další geometrická zobrazení.
Obsah |
Dějiny
Geometrické útvary patří vedle čísel k nejstarším zkoumaným předmětům matematiky, jednoduchou představu o některých z nich měli lidé zřejmě již v paleolitu, starší době kamenné.[9] V neolitu se pak různé útvary staly základem geometrické ornamentiky na více místech světa.[10] Další rozvoj přišel s nástupem prvních států v Mezopotámii a starověkém Egyptě, kde se poznatky o útvarech využívaly v zeměměřičství a stavebnictví. Babylóňané již znali zvláštní případy Pythagorovy věty a egyptští geometři uměli počítat obsah trojúhelníka i kruhu, přičemž jejich odhad čísla pí byl asi 3,1605.[10] K řadě poznatků se dospělo také ve starověké Indii a starověké Číně.[11]
Na vědeckou úroveň povznesli matematiku staří Řekové, především Eukleidés, autor první axiomatické teorie. Geometrických útvarů se týká řada jejich poznatků a úvah. Jmenovat lze například platónská tělesa (Platón je popsal a uvažoval o jejich hlubším smyslu, zatímco Eukleidés dokázal, že žádná další takto pravidelná tělesa již neexistují), Zénónovy paradoxy o nekonečném dělení úsečky nebo Archimédovy myšlenky o výpočtu objemu těles, předjímající pozdější integrální počet.[12] Útvarů se týkají také tři slavné problémy, které starověká matematika zanechala nevyřešené: trisekce úhlu, zdvojení krychle a kvadratura kruhu.[13]
Ve středověku rozvíjeli geometrii především Arabové; vznikly trigonometrické tabulky a díky arabskému astronomovi al-Battánímu se objevily první poznatky sférické trigonometrie.[14] V raném novověku rozvoj mechaniky podnítil zájem např. o výpočet těžiště.[15] Přelomový byl Descartův objev souřadnic, který umožnil vznik analytické geometrie a řešení geometrických problémů algebraickou a analytickou cestou.[16] K poznání geometrických útvarů tak bylo možno použít i diferenciální a integrální počet, který vznikl díky Isaacu Newtonovi a Gottfriedu Leibnizovi. Nové pohledy na geometrii umožnili v 19. století matematici jako Évariste Galois a Niels Henrik Abel (teorie grup, umožňující mj. analyzovat symetrie) či Nikolaj Ivanovič Lobačevskij a János Bolyai (neeukleidovská geometrie).[17] Teorie množin, již založil Georg Cantor, umožnila jednotný pohled na mnoho oblastí matematiky i řešení řady problémů spojených s otázkami nekonečna.[18]
Jako prostor, v němž geometrie pracovala, se po dvě tisíciletí bral výhradně prostor popsaný Euklidem v jeho Základech, jehož teorii[19] na konci 19. století axiomatizoval David Hilbert.[20] V 19. a 20. století se postupně objevily alternativy, jmenovitě neeukleidovské geometrie, umožňující vystihnout mj. geometrii zakřivených ploch,[21] a vícerozměrné prostory, vhodné např. pro popis časoprostoru.[22]
Základní geometrické útvary
- V některých učebnicích se uvádí jako základní geometrické útvary bod, přímka a rovina,[23][24] popř. i sám prostor.[2] Mezi základní geometrické útvary se někdy zahrnují i jiné útvary; ve školské matematice například kružnice, trojúhelník nebo čtverec.
- Bod je bezrozměrný dále nedělitelný element. Body se v učebnicích často značí velkými písmeny \(A\), \(B\), \(C\),…
- Přímka je abstrakce rovné čáry nulové šířky, jednorozměrný objekt, označuje se malým písmenem \(a\), \(b\), \(p\), \(q\) nebo \(\overline{A B}\) pomocí dvou různých bodů, které ji určují.
- Rovina je abstrakce ploché rovné desky nulové tloušťky, značí se písmeny řecké abecedy \(\alpha\), \(\beta\), \(\rho\), \(\pi\), nebo také \(\overline{A B C}\) pomocí tří různých bodů neležících na jedné přímce, které ji určují.
- V hilbertovské axiomatizaci geometrie se jsou bod, přímka a rovina spolu s některými vlastnostmi a vzájemnými vztahy definovány axiomaticky a další vlastnosti, útvary a tvrzení se odvozují z těchto stavebních prvků.
- V počítačové grafice se můžeme setkat s termínem grafické primitivum, což obvykle křivka, polygon a podobně.
Členění a příklady
Podle dimenze
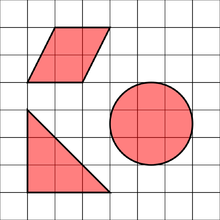
Rovinné útvary jsou takové útvary, jež celé leží v jedné rovině. Mimo jiné jde o:
- rovinné křivky – např. kuželosečky (kružnice, elipsa, parabola, hyperbola), cykloidy, řetězovky apod., ale i přímka a její nebodové části - polopřímky a úsečky
- (rovinné) obrazce – např. trojúhelník, čtyřúhelník a jiné mnohoúhelníky, kruh apod.
- rovinné fraktály - např. dračí křivka, Sierpinského koberec, Mandelbrotova množina apod.
Prostorové útvary jsou útvary, které nelze vnořit do žádné roviny. Jsou to například:
- prostorové křivky – např. šroubovice
- plochy v prostoru – např. kvadriky (přímkové plochy, kulová plocha, elipsoid, paraboloid, hyperboloid) apod.
- tělesa – např. mnohostěny (krychle, kvádr, hranol, jehlan), válec, kužel, koule apod.
- prostorové fraktály - např. Mengerova houba apod.
Dále lze uvažovat i vícerozměrný prostor a v něm vícerozměrné útvary. Příkladem mohou být čtyřrozměrná platónská tělesa.
Podle stupně polynomu
Analytická geometrie dělí útvary a své subdisciplíny podle stupně polynomů, popisujících útvar:[25]
- Analytická geometrie lineárních útvarů se zabývá útvary popsatelnými ve vhodně zvolené souřadné soustavě polynomy prvního stupně (v nichž souřadnice vystupují v první mocnině); příkladem je přímka (lze v rovině popsat rovnicí tvaru \(y = a x + b\), v prostoru soustavou \(b c(x - x_0) = a c(y - y_0) = a b(z-z_0)\)) či rovina (lze v prostoru popsat rovnicí tvaru \(a x + b y + c z + d = 0\)).
- Analytická geometrie kvadratických útvarů se zabývá útvary popsatelnými ve vhodně zvolené souřadné soustavě polynomy druhého stupně (v nichž jedna nebo více souřadnic vystupuje v druhé mocnině); příkladem jsou v rovině kuželosečky (např. parabolu lze popsat rovnicí tvaru \(y = a x^2 + b x + c\)), v prostoru kvadriky (např. hyperbolický paraboloid lze popsat rovnicí \(z-z_0 = (1/2p)(x- x_0)^2 - (1/2q)(y-y_0)^2\), kde \(pq > 0 \)).
- Algebraická geometrie se zabývá útvary popsatelnými polynomy obecného stupně.
Vlastnosti
Kromě základních definičních vlastností, jako jsou tvar, rozměry a poloha útvaru v prostoru, lze zkoumat i další vlastnosti geometrických útvarů. Například to jsou:
- Míry útvarů: Délka, obsah, objem, povrch a obvod, jsou-li definovány. Tyto veličiny zjednodušeně řečeno vyjadřují „velikost“ či „rozsah“ útvaru. Matematicky se určují jako Jordanova míra nebo obecněji Lebesgueova míra zkoumaného útvaru.
- Dimenze: Útvarům lze přiřadit číslo, které se nazývá počet rozměrů čili dimenze útvaru. Pro „běžné“ útvary je dimenze celé číslo: pro bod je to nula, pro přímku a obvyklé křivky 1, pro rovinu a běžné zakřivené plochy 2, pro prostorová tělesa jako koule a hranol 3. Existuje více způsobů definice dimenze; podle toho rozlišujeme např. topologickou dimenzi nebo různé fraktální dimenze (jako jsou Hausdorffova míra či Rényiho dimenze), jež pro speciální útvary zvané fraktály mohou být i neceločíselné.[26] (Pro fraktální útvary lze určovat i další speciální vlastnosti, např. lacunaritu,[27] měřící, nakolik fraktál vyplňuje prostor.)
- Symetrie čili souměrnost podle nějakého bodu, přímky či roviny, symetrie vzhledem k otočení či symetrie vůči změně měřítka (škálovací symetrie).
- Vnitřní body, vnější body, izolované body a hraniční body útvaru; hraniční bod je takový, že jeho každé okolí obsahuje alespoň jeden bod ležící v útvaru a současně alespoň jeden bod neležící v útvaru; množina všech hraničních bodů je hranice útvaru.
- Útvar může být otevřený, tedy obsahovat pouze vnitřní body. To znamená, že každý bod útvaru má kolem sebe nějaké okolí, jež obsahuje pouze body tohoto útvaru. Otevřený útvar tedy neobsahuje svou hranici.
- Útvar může být uzavřený, tedy obsahovat všechny své hromadné body; každá konvergentní posloupnost bodů útvaru má limitu, která rovněž patří do útvaru. Uzavřený útvar tedy obsahuje všechny své hraniční body. Útvar může být zároveň otevřený i uzavřený (to splňují prázdná množina a celý prostor) a naopak nemusí být ani otevřený, ani uzavřený (např. polootevřená úsečka). „Uzavřená křivka“ ovšem zpravidla znamená „křivka, jejíž počáteční bod se shoduje s koncovým,“ nejde tedy o uzavřenost v množinovém smyslu.
- Útvar může být souvislý; to znamená, že mezi libovolnými dvěma jeho body existuje souvislá čára, která leží celá v útvaru.
- Útvar může být konvexní; to znamená, že úsečka mezi libovolnými dvěma jeho body leží celá v útvaru. Z toho je patrné, že konvexní útvar musí být souvislý.
Vztahy mezi útvary
- Podrobnější informace naleznete na stránce: Analytická geometrie#Vzájemná poloha geometrických útvarů
Kromě obecných logických vztahů (existence, rovnost) používá Hilbertovská axiomatizace geometrie tři různé vztahy mezi geometrickými objekty:[28]
- Incidence, což znamená vlastnost „ležet na“, „ležet v“, „být prvkem“. Značí se \(\in\) a její negace jako \({\not \in}\). Například \(A\in p\) znamená „bod A leží na přímce p“.
- Vlastnost „ležet mezi“, např. bod A leží mezi body X a Y na přímce p.
- Shodnost, tedy schopnost útvarů se po vhodné transformaci zachovávající vzdálenosti ztotožnit. Týká se např. úseček (stejná délka) nebo úhlů (stejná velikost úhlu). Značí se \(\cong\). Například \(\triangle \mathrm{ABC} \cong \triangle \mathrm{DEF}\) čteme „trojúhelník ABC je shodný s trojúhelníkem DEF“ a znamená to, že oba trojúhelníky mají stejné délky stran a velikosti úhlů.
Vedle shodnosti existují další geometrická zobrazení, zejména podobnost, afinní zobrazení a topologická zobrazení. Jelikož útvary jsou množiny, je možno o nich také hovořit množinovým jazykem a zkoumat například jejich průnik a sjednocení.
Zobecnění
Existují různá matematická zobecnění pojmu geometrický útvar. Topologie se zabývá vlastnostmi množin, které se nemění při spojitých transformacích a topologický prostor je zobecněním pojmu tvar. Vlastnosti geometrických objektů, které se nemění při difeomorfizmech studuje diferenciální topologie a vlastnosti, které se nemění při homotopiích, studuje algebraická topologie. Vlastnosti útvarů, které se zachovávají při různých transformacích, se nazývají invarianty. V algebraické topologii jsou to například díry různých dimenzí (například kruh bez bodu má díru, plný kruh nikoliv). Invarianty, které formalizují a popisují typy a počty děr, jsou homotopické grupy a homologické grupy.[29]
Literatura
- KLAPKA, Jiří. Jak se studují geometrické útvary v prostoru?. Část první. Praha : Jednota československých matematiků a fysiků, 1947.
- KLAPKA, Jiří. Jak se studují geometrické útvary v prostoru?. II. část. Praha : Jednota československých matematiků a fysiků, 1947.
- VYŠÍN, Jan. Konvexní útvary. Praha : Mladá fronta, 1964.
- JUKL, Marek. Analytická geometrie lineárních útvarů. 2. vyd. Olomouc : Univerzita Palackého v Olomouci, 2008. ISBN 978-80-244-2148-3.
- PECH, Pavel. Analytická geometrie lineárních útvarů. České Budějovice : Jihočeská univerzita, 2004. ISBN 80-7040-741-7.
Reference
- ↑ Slovník školské matematiky, SPN Praha, 1981, s. 220-221
- ↑ 2,0 2,1 2,2 2,3 2,4 BARTSCH, Hans-Jochen, Matematické vzorce, SNTL Praha, 1983, s. 283
- ↑ POLÁK, Josef, Přehled středoškolské matematiky, Praha : Prometheus, 2008, ISBN 978-80-7196-356-1, s. 414
- ↑ Tristan Needham, Anschauliche Funktionentheorie, Oldenbourg Wissenschaftsverlag, 2001, str. 36,37
- ↑ Scott Milross Buchanan, Poetry and mathematics, Lippincott; [1st Keystone ed.] edition, 1962, str. 48
- ↑ Rudolph Berlinger, Philosophische Perspektiven, sv. 3, Frankfurt a. M., Verlag Vittorio Klostermann, 1971, str. 19
- ↑ Ottův slovník naučný, heslo Geometrie, svazek 10, str. 34, Ottův slovník naučný: Illustrovaná encyklopédie obecných vědomostí, heslo Geometrie
- ↑ Allan Bluman, Pre-Algebra DeMYSTiFieD, McGraw-Hill Professional, 2010, (s.e.), str. 198
- ↑ ŠALÁT, Tibor. Malá encyklopédia matematiky. 3. vyd. Bratislava : Obzor, 1981. Dostupné online. S. 7. (slovensky)
- ↑ 10,0 10,1 Šalát, s. 8
- ↑ Šalát, s. 9
- ↑ Šalát, s. 10–11
- ↑ Šalát, s. 10
- ↑ Šalát, s. 12
- ↑ Šalát, s. 13
- ↑ Šalát, s. 14
- ↑ Šalát, s. 17–19
- ↑ Šalát, s. 18
- ↑ HILBERT, David, The Foundations of Geometry, The Open Court Publishing Company, La Salle, Illinois, 1950, s. 2–15, on-line
- ↑ MLODINOW, Leonard, Euclid's Window: The Story of Geometry from Parallel Lines to Hyperspace, Touchstone 2002, ISBN 0-684-86523-8, s. 3–52, 143–152
- ↑ Mlodinow, s. 95–142
- ↑ Mlodinow, s. 153–216
- ↑ Matematika pro gymnázia. Stereometrie. ISBN 978-80-7196-389-9, s. 8
- ↑ POMYKALOVÁ, Eva. Deskriptivní geometrie pro střední školy. Praha : Prometheus, 2010. ISBN 978-80-7196-400-1. S. 11.
- ↑ Kol.: Aplikovaná matematika 1, SNTL, Praha 1977, s. 83–84
- ↑ VACHTL, Pavel, Fraktály a chaos, Natura, on-line
- ↑ Tolle,C.R. McJunkin,T.R. Rohrbaugh,D.T. a LaViolette,R.A., Lacunarity definition for ramified data sets based on optimal cover, Physica D: Nonlinear Phenomena Volume 179, Issues 3-4, 15 May 2003, s. 129-152. DOI=http://dx.doi.org/10.1016/S0167-2789(03)00029-0
- ↑ Aplikovaná matematika 1, s. 420–422
- ↑ HATCHER, Allen. Algebraic Topology. [s.l.] : Cambridge University Press, 2002. ISBN 0-521-79160-X. (anglicky) Dostupné online
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |



